Advertisements
Advertisements
प्रश्न
बिंदुओं A(–5, 6), B(–4, –2) और C(7, 5) से बनने वाले त्रिभुज का प्रकार बताइए।
उत्तर
त्रिभुज का प्रकार जानने के लिए सबसे पहले हम तीनों भुजाओं की लंबाई निर्धारित करते हैं और देखते हैं कि त्रिभुज की जो भी स्थिति इन भुजाओं से संतुष्ट होती है।
अब, दो बिंदुओं के बीच दूरी सूत्र का उपयोग करते हुए,
AB = `sqrt((-4 + 5)^2 + (-2 - 6)^2` ...`[∵ d = sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)]`
= `sqrt((1)^2 + (-8)^2`
= `sqrt(1 + 64)`
= `sqrt(65)`
BC = `sqrt((7 + 4)^2 + (5 + 2)^2`
= `sqrt((11)^2 + (7)^2`
= `sqrt(121 + 49)`
= `sqrt(170)`
और CA = `sqrt((-5 - 7)^2 + (6 - 5)^2`
= `sqrt((-12)^2 + (1)^2`
= `sqrt(144 + 1)`
= `sqrt(145)`
हमने देखा कि,
AB ≠ BC ≠ CA
और पाइथागोरस की स्थिति को ΔABC में न रखें।
अर्थात, (कर्ण)2 = (आधार)2 + (लंबवत)2
अतः, अभीष्ट त्रिभुज विषमबाहु है क्योंकि इसकी सभी भुजाएँ समान नहीं हैं अर्थात एक दूसरे से भिन्न हैं।
APPEARS IN
संबंधित प्रश्न
नीचे दिए गए बिंदु एकरेखीय हैं या नहीं? इसकी जाँच कीजिए।
L(-2, 3), M(1, -3), N(5, 4)
नीचे दिए गए बिंदु एकरेखीय हैं या नहीं? इसकी जाँच कीजिए।
R(0, 3), D(2, 1), S(3, -1)
जाँच कीजिए कि बिंदु P(-2, 2), Q(2, 2) और R(2, 7) समकोण त्रिभुज के शीर्षबिंदु हैं।
बिंदुओं (0,0) और (36, 15) के बीच की दूरी ज्ञात कीजिए। क्या अब आप अनुच्छेद 7.2 में दिए दोनों शहरों A और B के बीच की दूरी ज्ञात कर सकते हैं?
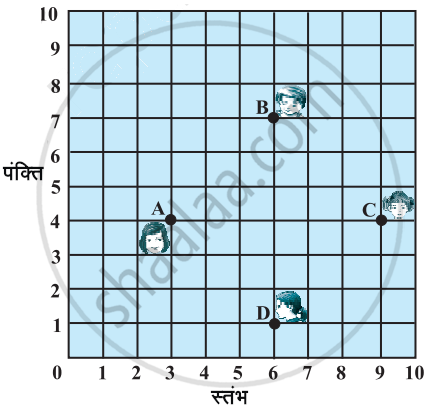
किसी कक्षा में, चार मित्र बिंदुओं A, B, C और D पर बैठे हुए हैं, जैसाकि आकृति में दर्शाया गया है। चंपा और चमेली कक्षा के अंदर आती हैं और कुछ मिनट तक देखने के बाद, चंपा चमेली से पूछती है, 'क्या तुम नहीं सोचती हो कि ABCD एक वर्ग है?' चमेली इससे सहमत नहीं है। दूरी सूत्र का प्रयोग करके, बताइए कि इनमें कौन सही है?
x-अक्ष पर वह बिंदु ज्ञात कीजिए जो (2, -5) और (-2, 9) से समदूरस्थ हैं।
बिंदुओं (0, 5) और (–5, 0) के बीच की दूरी ______ है।
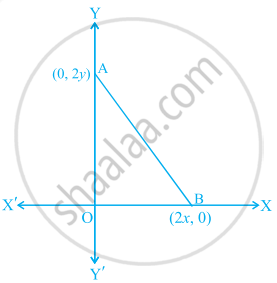
आकृति में दर्शाए गए त्रिभुज AOB के तीनों शीर्षो से समदूरस्थ बिंदु के निर्देशांक ______ हैं।
मूलबिंदु को केंद्र मान कर खींचा गया एक वृत्त बिंदु `(13/2, 0)` से होकर जाता है। तब, वृत्त के अभ्यंतर में निम्नलिखित बिंदु स्थित नहीं ______ है।
x-अक्ष पर स्थित ऐसे बिंदु ज्ञात कीजिए, जो बिंदु (7, – 4) से `2sqrt(5)` की दूरी पर हैं। ऐसे कितने बिंदु हैं?
