Advertisements
Advertisements
प्रश्न
Consider f: `R_+ -> [-5, oo]` given by `f(x) = 9x^2 + 6x - 5`. Show that f is invertible with `f^(-1) (y) ((sqrt(y + 6)-1)/3)`
Hence Find
1) `f^(-1)(10)`
2) y if `f^(-1) (y) = 4/3`
where R+ is the set of all non-negative real numbers.
उत्तर
f: `R_+ -> [-5, oo]` given by `f(x) = 9x^2 + 6x - 5`
To show: f is one-one and onto.
Let us assume that f is not one-one.
Therefore there exist two or more numbers for which images are same.
For x1, x2 ∈ R+ and x1 ≠ x2
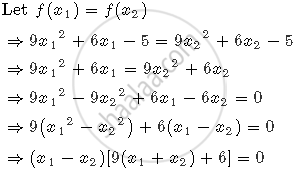
Since x1 and x2 are positive,
9(x1 + x2) + 6 > 0
∴ x1 − x2 = 0⇒ x1 = x2
Therefore, it contradicts our assumption.
Hence the function f is one-one.
Now, let is prove that f is onto.
A function f : X → Y is onto if for every y ∈ Y, there exist a pre-image in X.
f(x) = 9x2 + 6x −5
= 9x2 + 6x + 1 - 6
=(3x + 1)2 - 6
Now, for all x ∈ R+ or [0,∞), f(x) ∈ [−5, ∞)
∴ Range = co-domain.
Hence, f is onto.
Therefore, function f is invertible.
Now, let y = 9x2 + 6x − 5
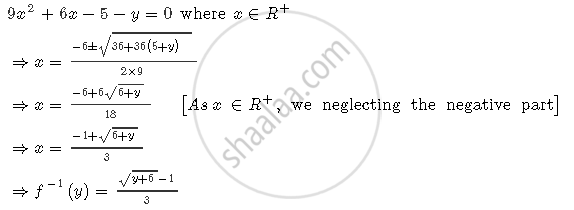
1) `f^(-1) (10) = (sqrt(10+6)-1)/3 = (4-1)/3 = 1`
2) `f^(-1) (y) = 4/3`
`:.(sqrt(y + 6) -1)/3 = 4/3`
`=> sqrt(y + 6)-1 = 4`
`=> sqrt(y+6) = 5`
`=> y + 6 = 25`
=> y = 19
APPEARS IN
संबंधित प्रश्न
If the function f : R → R be defined by f(x) = 2x − 3 and g : R → R by g(x) = x3 + 5, then find the value of (fog)−1 (x).
Let f: {1, 3, 4} → {1, 2, 5} and g: {1, 2, 5} → {1, 3} be given by f = {(1, 2), (3, 5), (4, 1)} and g = {(1, 3), (2, 3), (5, 1)}. Write down gof.
Let f, g and h be functions from R to R. Show that
`(f + g)oh = foh + goh`
`(f.g)oh = (foh).(goh)`
Find gof and fog, if f(x) = |x| and g(x) = |5x - 2|
Find gof and fog, if `f(x) = 8x^3` and `g(x) = x^(1/3)`
if f(x) = `(4x + 3)/(6x - 4), x ≠ 2/3` show that fof(x) = x, for all x ≠ 2/3 . What is the inverse of f?
Consider f: R+ → [−5, ∞) given by f(x) = 9x2 + 6x − 5. Show that f is invertible with `f^(-1)(y) = ((sqrt(y +6) - 1)/3)`
Consider f: {1, 2, 3} → {a, b, c} given by f(1) = a, f(2) = b and f(3) = c. Find f−1 and show that (f−1)−1 = f.
Let f: W → W be defined as f(n) = n − 1, if is odd and f(n) = n + 1, if n is even. Show that f is invertible. Find the inverse of f. Here, W is the set of all whole numbers.
Let f : W → W be defined as f(x) = x − 1 if x is odd and f(x) = x + 1 if x is even. Show that f is invertible. Find the inverse of f, where W is the set of all whole numbers.
If f : R → R, f(x) = x3 and g: R → R , g(x) = 2x2 + 1, and R is the set of real numbers, then find fog(x) and gof (x)
Is g = {(1, 1), (2, 3), (3, 5), (4, 7)} a function? If g is described by g (x) = αx + β, then what value should be assigned to α and β
Let f: N → R be the function defined by f(x) = `(2x - 1)/2` and g: Q → R be another function defined by g(x) = x + 2. Then (g o f) `3/2` is ______.
Let f: R → R be the function defined by f(x) = sin (3x+2) ∀ x ∈ R. Then f is invertible.
Every function is invertible.
If f(x) = `(3"x" + 2)/(5"x" - 3)` then (fof)(x) is ____________.
Let f : R – `{3/5}`→ R be defined by f(x) = `(3"x" + 2)/(5"x" - 3)` Then ____________.
Which one of the following functions is not invertible?
The inverse of the function `"y" = (10^"x" - 10^-"x")/(10^"x" + 10^-"x")` is ____________.
`f : x -> sqrt((3x^2 - 1)` and `g : x -> sin (x)` then `gof : x ->`?
The domain of definition of f(x) = log x2 – x + 1) (2x2 – 7x + 9) is:-
Domain of the function defined by `f(x) = 1/sqrt(sin^2 - x) log_10 (cos^-1 x)` is:-
Let A = `{3/5}` and B = `{7/5}` Let f: A → B: f(x) = `(7x + 4)/(5x - 3)` and g:B → A: g(y) = `(3y + 4)/(5y - 7)` then (gof) is equal to
Let 'D' be the domain of the real value function on Ir defined by f(x) = `sqrt(25 - x^2)` the D is :-
If f: A → B and G B → C are one – one, then g of A → C is
If f(x) = [4 – (x – 7)3]1/5 is a real invertible function, then find f–1(x).
