Advertisements
Advertisements
Question
Consider f: `R_+ -> [-5, oo]` given by `f(x) = 9x^2 + 6x - 5`. Show that f is invertible with `f^(-1) (y) ((sqrt(y + 6)-1)/3)`
Hence Find
1) `f^(-1)(10)`
2) y if `f^(-1) (y) = 4/3`
where R+ is the set of all non-negative real numbers.
Advertisements
Solution
f: `R_+ -> [-5, oo]` given by `f(x) = 9x^2 + 6x - 5`
To show: f is one-one and onto.
Let us assume that f is not one-one.
Therefore there exist two or more numbers for which images are same.
For x1, x2 ∈ R+ and x1 ≠ x2
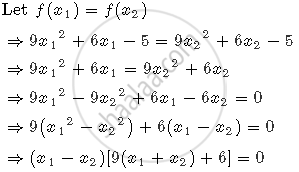
Since x1 and x2 are positive,
9(x1 + x2) + 6 > 0
∴ x1 − x2 = 0⇒ x1 = x2
Therefore, it contradicts our assumption.
Hence the function f is one-one.
Now, let is prove that f is onto.
A function f : X → Y is onto if for every y ∈ Y, there exist a pre-image in X.
f(x) = 9x2 + 6x −5
= 9x2 + 6x + 1 - 6
=(3x + 1)2 - 6
Now, for all x ∈ R+ or [0,∞), f(x) ∈ [−5, ∞)
∴ Range = co-domain.
Hence, f is onto.
Therefore, function f is invertible.
Now, let y = 9x2 + 6x − 5
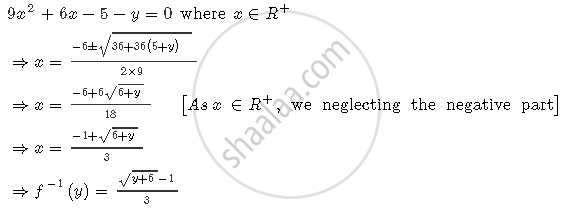
1) `f^(-1) (10) = (sqrt(10+6)-1)/3 = (4-1)/3 = 1`
2) `f^(-1) (y) = 4/3`
`:.(sqrt(y + 6) -1)/3 = 4/3`
`=> sqrt(y + 6)-1 = 4`
`=> sqrt(y+6) = 5`
`=> y + 6 = 25`
=> y = 19
APPEARS IN
RELATED QUESTIONS
If the function f : R → R be defined by f(x) = 2x − 3 and g : R → R by g(x) = x3 + 5, then find the value of (fog)−1 (x).
Find gof and fog, if f(x) = 8x3 and `g(x) = x^(1/3)`.
State with reason whether following functions have inverse
h: {2, 3, 4, 5} → {7, 9, 11, 13} with h = {(2, 7), (3, 9), (4, 11), (5, 13)}
Consider f: R → R given by f(x) = 4x + 3. Show that f is invertible. Find the inverse of f.
Let f: X → Y be an invertible function. Show that f has unique inverse. (Hint: suppose g1 and g2 are two inverses of f. Then for all y ∈ Y, fog1(y) = IY(y) = fog2(y). Use one-one ness of f).
Consider f: {1, 2, 3} → {a, b, c} given by f(1) = a, f(2) = b and f(3) = c. Find f−1 and show that (f−1)−1 = f.
Let `f: R - {-4/3} → R` be a function defined as `f(x) = (4x)/(3x + 4)`. The inverse of f is map g: Range `f → R - {-4/3}` given by
Let f: W → W be defined as f(n) = n − 1, if is odd and f(n) = n + 1, if n is even. Show that f is invertible. Find the inverse of f. Here, W is the set of all whole numbers.
If f: R → R is defined by f(x) = x2 − 3x + 2, find f(f(x)).
Let f : W → W be defined as f(x) = x − 1 if x is odd and f(x) = x + 1 if x is even. Show that f is invertible. Find the inverse of f, where W is the set of all whole numbers.
If f : R → R, f(x) = x3 and g: R → R , g(x) = 2x2 + 1, and R is the set of real numbers, then find fog(x) and gof (x)
Let f: R → R be defined by f(x) = 3x 2 – 5 and g: R → R by g(x) = `x/(x^2 + 1)` Then gof is ______.
Let f: A → B and g: B → C be the bijective functions. Then (g o f)–1 is ______.
Let f: N → R be the function defined by f(x) = `(2x - 1)/2` and g: Q → R be another function defined by g(x) = x + 2. Then (g o f) `3/2` is ______.
Let f = {(1, 2), (3, 5), (4, 1) and g = {(2, 3), (5, 1), (1, 3)}. Then g o f = ______ and f o g = ______.
Every function is invertible.
If f(x) = (ax2 + b)3, then the function g such that f(g(x)) = g(f(x)) is given by ____________.
Let f : N → R : f(x) = `((2"x"−1))/2` and g : Q → R : g(x) = x + 2 be two functions. Then, (gof) `(3/2)` is ____________.
If f(x) = (ax2 – b)3, then the function g such that f{g(x)} = g{f(x)} is given by ____________.
Consider the function f in `"A = R" - {2/3}` defiend as `"f"("x") = (4"x" + 3)/(6"x" - 4)` Find f-1.
If f is an invertible function defined as f(x) `= (3"x" - 4)/5,` then f-1(x) is ____________.
`f : x -> sqrt((3x^2 - 1)` and `g : x -> sin (x)` then `gof : x ->`?
Domain of the function defined by `f(x) = 1/sqrt(sin^2 - x) log_10 (cos^-1 x)` is:-
Let A = `{3/5}` and B = `{7/5}` Let f: A → B: f(x) = `(7x + 4)/(5x - 3)` and g:B → A: g(y) = `(3y + 4)/(5y - 7)` then (gof) is equal to
Let 'D' be the domain of the real value function on Ir defined by f(x) = `sqrt(25 - x^2)` the D is :-
If f(x) = [4 – (x – 7)3]1/5 is a real invertible function, then find f–1(x).
