Advertisements
Advertisements
Question
If the sum of lengths of hypotenuse and a side of a right angled triangle is given, show that area of triangle is maximum, when the angle between them is π/3.
Solution
Let ABC be the right angled triangle with BC = x , AC = y such that x + y = k, where k is any constant. Let θ be the angle between the base and the hypotenuse.
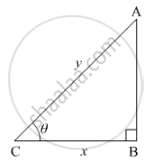
Let A be the area of the triangle.
`A=1/2xxBC×AC=1/2xsqrt(y^2−x^2)`
`⇒A^2=x^2/4(y^2−x^2)`
`⇒A^2=x^2/4[(k−x)^2−x^2]`
`⇒A^2=(k^2x^2−2kx^3)/4 .....(1)`
Differentiating w.r.t. x, we get
`2A(dA)/(dx)=(2k^2x−6kx^2)/4 .....(2)`
`⇒(dA)/(dx)=(k^2x−3kx^2)/(4A)`
For maximum or minimum,
`(dA)/(dx)=0`
`⇒(k^2x−3kx^2)/(4A)=0`
`⇒x=k/3`
Differentiating (2) w.r.t. x, we get
`2((dA)/(dx))^2+2A(d^2A)/(dx^2)=(2k^2−12kx)/4 .....(3)`
Substituting `(dA)/(dx)=0 and x=k/3` in (3), we get
`(d^2A)/(dx^2)=−k^2/(4A)<0`
Thus, A is maximum when x=k/3.
`x=k/3⇒y=k−k/3=(2k)/3 [∵x+y=k]`
`∴ cosθ=x/y`
`⇒cosθ=(k/3)/((2k)/3)=1/2`
`⇒θ=π/3`
APPEARS IN
RELATED QUESTIONS
Find the maximum and minimum value, if any, of the function given by f(x) = |x + 2| − 1.
Find the local maxima and local minima, if any, of the following functions. Find also the local maximum and the local minimum values, as the case may be:
`f(x) = xsqrt(1-x), x > 0`
A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the length of the two pieces so that the combined area of the square and the circle is minimum?
Find the points at which the function f given by f (x) = (x – 2)4 (x + 1)3 has
- local maxima
- local minima
- point of inflexion
Divide the number 30 into two parts such that their product is maximum.
Find the volume of the largest cylinder that can be inscribed in a sphere of radius ‘r’ cm.
Solve the following : A window is in the form of a rectangle surmounted by a semicircle. If the perimeter be 30 m, find the dimensions so that the greatest possible amount of light may be admitted.
Solve the following : Show that the height of a right circular cylinder of greatest volume that can be inscribed in a right circular cone is one-third of that of the cone.
Determine the maximum and minimum value of the following function.
f(x) = `x^2 + 16/x`
A rod of 108 m long is bent to form a rectangle. Find it’s dimensions when it’s area is maximum.
The maximum volume of a right circular cylinder if the sum of its radius and height is 6 m is ______.
If f(x) = 3x3 - 9x2 - 27x + 15, then the maximum value of f(x) is _______.
The function y = 1 + sin x is maximum, when x = ______
The sum of two non-zero numbers is 6. The minimum value of the sum of their reciprocals is ______.
Find all the points of local maxima and local minima of the function f(x) = `- 3/4 x^4 - 8x^3 - 45/2 x^2 + 105`
Let f have second derivative at c such that f′(c) = 0 and f"(c) > 0, then c is a point of ______.
Find the dimensions of the rectangle of perimeter 36 cm which will sweep out a volume as large as possible, when revolved about one of its sides. Also find the maximum volume.
If the sum of the surface areas of cube and a sphere is constant, what is the ratio of an edge of the cube to the diameter of the sphere, when the sum of their volumes is minimum?
AB is a diameter of a circle and C is any point on the circle. Show that the area of ∆ABC is maximum, when it is isosceles.
Find the points of local maxima and local minima respectively for the function f(x) = sin 2x - x, where `-pi/2 le "x" le pi/2`
Find the maximum profit that a company can make, if the profit function is given by P(x) = 41 + 24x – 18x2.
The function `f(x) = x^3 - 6x^2 + 9x + 25` has
The maximum value of `[x(x - 1) + 1]^(2/3), 0 ≤ x ≤ 1` is
If y = alog|x| + bx2 + x has its extremum values at x = –1 and x = 2, then ______.
If the function y = `(ax + b)/((x - 4)(x - 1))` has an extremum at P(2, –1), then the values of a and b are ______.
The minimum value of 2sinx + 2cosx is ______.
A straight line is drawn through the point P(3, 4) meeting the positive direction of coordinate axes at the points A and B. If O is the origin, then minimum area of ΔOAB is equal to ______.
Check whether the function f : R `rightarrow` R defined by f(x) = x3 + x, has any critical point/s or not ? If yes, then find the point/s.
If Mr. Rane order x chairs at the price p = (2x2 - 12x - 192) per chair. How many chairs should he order so that the cost of deal is minimum?
Solution: Let Mr. Rane order x chairs.
Then the total price of x chairs = p·x = (2x2 - 12x- 192)x
= 2x3 - 12x2 - 192x
Let f(x) = 2x3 - 12x2 - 192x
∴ f'(x) = `square` and f''(x) = `square`
f'(x ) = 0 gives x = `square` and f''(8) = `square` > 0
∴ f is minimum when x = 8
Hence, Mr. Rane should order 8 chairs for minimum cost of deal.
