Question

If the sum of lengths of hypotenuse and a side of a right angled triangle is given, show that area of triangle is maximum, when the angle between them is π/3.

Answer 1

Let ABC be the right angled triangle with BC = x , AC = y such that x + y = k, where k is any constant. Let θ be the angle between the base and the hypotenuse.

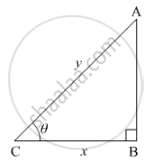
Let A be the area of the triangle.

`A=1/2xxBC×AC=1/2xsqrt(y^2−x^2)`

`⇒A^2=x^2/4(y^2−x^2)`

`⇒A^2=x^2/4[(k−x)^2−x^2]`

`⇒A^2=(k^2x^2−2kx^3)/4           .....(1)`

Differentiating w.r.t. x, we get

`2A(dA)/(dx)=(2k^2x−6kx^2)/4       .....(2)`

`⇒(dA)/(dx)=(k^2x−3kx^2)/(4A)`

For maximum or minimum,

`(dA)/(dx)=0`

`⇒(k^2x−3kx^2)/(4A)=0`

`⇒x=k/3`

Differentiating (2) w.r.t. x, we get

`2((dA)/(dx))^2+2A(d^2A)/(dx^2)=(2k^2−12kx)/4        .....(3)`

Substituting `(dA)/(dx)=0 and x=k/3`  in (3), we get

`(d^2A)/(dx^2)=−k^2/(4A)<0`

Thus, A is maximum when x=k/3.

`x=k/3⇒y=k−k/3=(2k)/3        [∵x+y=k]`

`∴ cosθ=x/y`

`⇒cosθ=(k/3)/((2k)/3)=1/2`

`⇒θ=π/3`