Advertisements
Advertisements
Question
AB is a diameter of a circle and C is any point on the circle. Show that the area of ∆ABC is maximum, when it is isosceles.
Solution
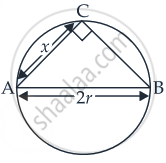
Let AB be the diameter and C be any point on the circle with radius r.
∠ACB = 90° ......[angle in the semi-circle is 90°]
Let AC = x
∴ BC = `sqrt("AB"^2 - "AC"^2)`
⇒ BC = `sqrt((2"r")^2 - x^2)`
⇒ BC = `sqrt(4"r"^2 - x^2)` ....(i)
Now area of ∆ABC
A = `1/2 xx "AC" xx "BC"`
⇒ A = `1/2 x * sqrt(4"r"^2 - x^2)`
Squaring both sides, we get
A2 = `1/4 x^2 (4"r"^2 - x^2)`
Let A2 = Z
∴ Z = `1/4 x^2(4"r"^2 - x^2)`
⇒ Z = `1/4(4x^2"r"^2 - x^4)`
Differentiating both sides w.r.t. x, we get
`"dZ"/"dx" = 1/4 [8x"r"^2 - 4x^3]` ....(ii)
For local maxima and local minima `"dZ"/"dx"` = 0
∴ `1/4 [8x"r"^2 - 4x^3]` = 0
⇒ `x[2"r"^2 - x^2]` = 0
x ≠ 0
∴ 2r2 – x2 = 0
⇒ x2 = 2r2
⇒ x = `sqrt(2)"r"`
= AC
Now from equation (i) we have
BC = `sqrt(4"r"^2 - 2"r"^2)`
⇒ BC = `sqrt(2"r"^2)`
⇒ BC = `sqrt(2)"r"`
So AC = BC
Hence, ∆ABC is an isosceles triangle.
Differentiating equation (ii) w.r.t. x, we get
`("d"^2"Z")/("dx"^2) = 1/4 [8"r"^2 - 12x^2]`
Put x = `sqrt(2)"r"`
∴ `("d"^2"Z")/("dx"^2) = 1/4 [8"r"^2 - 12 xx 2"r"^2]`
= `1/4[8"r"^2 - 24"r"^2]`
= `1/4 xx (-16"r"^2)`
= `-4"r"^2 < 0` maxima
Hence, the area of ∆ABC is maximum when it is an isosceles triangle.
APPEARS IN
RELATED QUESTIONS
If `f'(x)=k(cosx-sinx), f'(0)=3 " and " f(pi/2)=15`, find f(x).
If the sum of lengths of hypotenuse and a side of a right angled triangle is given, show that area of triangle is maximum, when the angle between them is π/3.
Find the maximum and minimum value, if any, of the following function given by f(x) = (2x − 1)2 + 3.
Find the maximum and minimum value, if any, of the following function given by g(x) = − |x + 1| + 3.
Find the points at which the function f given by f (x) = (x – 2)4 (x + 1)3 has
- local maxima
- local minima
- point of inflexion
Find the point on the straight line 2x+3y = 6, which is closest to the origin.
A rectangle is inscribed in a semicircle of radius r with one of its sides on the diameter of the semicircle. Find the dimensions of the rectangle to get the maximum area. Also, find the maximum area.
A ball is thrown in the air. Its height at any time t is given by h = 3 + 14t – 5t2. Find the maximum height it can reach.
The perimeter of a triangle is 10 cm. If one of the side is 4 cm. What are the other two sides of the triangle for its maximum area?
Find the volume of the largest cylinder that can be inscribed in a sphere of radius ‘r’ cm.
Solve the following : Show that of all rectangles inscribed in a given circle, the square has the maximum area.
Solve the following : Show that the height of a right circular cylinder of greatest volume that can be inscribed in a right circular cone is one-third of that of the cone.
If f(x) = x.log.x then its maximum value is ______.
A rod of 108 m long is bent to form a rectangle. Find it’s dimensions when it’s area is maximum.
The minimum value of the function f(x) = 13 - 14x + 9x2 is ______
Find the dimensions of the rectangle of perimeter 36 cm which will sweep out a volume as large as possible, when revolved about one of its sides. Also find the maximum volume.
If the sum of the surface areas of cube and a sphere is constant, what is the ratio of an edge of the cube to the diameter of the sphere, when the sum of their volumes is minimum?
The maximum value of sin x . cos x is ______.
Find all the points of local maxima and local minima of the function f(x) = (x - 1)3 (x + 1)2
Find both the maximum and minimum values respectively of 3x4 - 8x3 + 12x2 - 48x + 1 on the interval [1, 4].
The function `"f"("x") = "x" + 4/"x"` has ____________.
The point on the curve `x^2 = 2y` which is nearest to the point (0, 5) is
A wire of length 36 m is cut into two pieces, one of the pieces is bent to form a square and the other is bent to form a circle. If the sum of the areas of the two figures is minimum, and the circumference of the circle is k (meter), then `(4/π + 1)`k is equal to ______.
If the point (1, 3) serves as the point of inflection of the curve y = ax3 + bx2 then the value of 'a ' and 'b' are ______.
A rod AB of length 16 cm. rests between the wall AD and a smooth peg, 1 cm from the wall and makes an angle θ with the horizontal. The value of θ for which the height of G, the midpoint of the rod above the peg is minimum, is ______.
A straight line is drawn through the point P(3, 4) meeting the positive direction of coordinate axes at the points A and B. If O is the origin, then minimum area of ΔOAB is equal to ______.
The rectangle has area of 50 cm2. Complete the following activity to find its dimensions for least perimeter.
Solution: Let x cm and y cm be the length and breadth of a rectangle.
Then its area is xy = 50
∴ `y =50/x`
Perimeter of rectangle `=2(x+y)=2(x+50/x)`
Let f(x) `=2(x+50/x)`
Then f'(x) = `square` and f''(x) = `square`
Now,f'(x) = 0, if x = `square`
But x is not negative.
∴ `x = root(5)(2) "and" f^('')(root(5)(2))=square>0`
∴ by the second derivative test f is minimum at x = `root(5)(2)`
When x = `root(5)(2),y=50/root(5)(2)=root(5)(2)`
∴ `x=root(5)(2) "cm" , y = root(5)(2) "cm"`
Hence, rectangle is a square of side `root(5)(2) "cm"`
A running track of 440 m is to be laid out enclosing a football field. The football field is in the shape of a rectangle with a semi-circle at each end. If the area of the rectangular portion is to be maximum,then find the length of its sides. Also calculate the area of the football field.
Determine the minimum value of the function.
f(x) = 2x3 – 21x2 + 36x – 20
