Advertisements
Advertisements
प्रश्न
AB is a diameter of a circle and C is any point on the circle. Show that the area of ∆ABC is maximum, when it is isosceles.
उत्तर
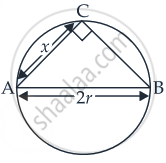
Let AB be the diameter and C be any point on the circle with radius r.
∠ACB = 90° ......[angle in the semi-circle is 90°]
Let AC = x
∴ BC = `sqrt("AB"^2 - "AC"^2)`
⇒ BC = `sqrt((2"r")^2 - x^2)`
⇒ BC = `sqrt(4"r"^2 - x^2)` ....(i)
Now area of ∆ABC
A = `1/2 xx "AC" xx "BC"`
⇒ A = `1/2 x * sqrt(4"r"^2 - x^2)`
Squaring both sides, we get
A2 = `1/4 x^2 (4"r"^2 - x^2)`
Let A2 = Z
∴ Z = `1/4 x^2(4"r"^2 - x^2)`
⇒ Z = `1/4(4x^2"r"^2 - x^4)`
Differentiating both sides w.r.t. x, we get
`"dZ"/"dx" = 1/4 [8x"r"^2 - 4x^3]` ....(ii)
For local maxima and local minima `"dZ"/"dx"` = 0
∴ `1/4 [8x"r"^2 - 4x^3]` = 0
⇒ `x[2"r"^2 - x^2]` = 0
x ≠ 0
∴ 2r2 – x2 = 0
⇒ x2 = 2r2
⇒ x = `sqrt(2)"r"`
= AC
Now from equation (i) we have
BC = `sqrt(4"r"^2 - 2"r"^2)`
⇒ BC = `sqrt(2"r"^2)`
⇒ BC = `sqrt(2)"r"`
So AC = BC
Hence, ∆ABC is an isosceles triangle.
Differentiating equation (ii) w.r.t. x, we get
`("d"^2"Z")/("dx"^2) = 1/4 [8"r"^2 - 12x^2]`
Put x = `sqrt(2)"r"`
∴ `("d"^2"Z")/("dx"^2) = 1/4 [8"r"^2 - 12 xx 2"r"^2]`
= `1/4[8"r"^2 - 24"r"^2]`
= `1/4 xx (-16"r"^2)`
= `-4"r"^2 < 0` maxima
Hence, the area of ∆ABC is maximum when it is an isosceles triangle.
APPEARS IN
संबंधित प्रश्न
Examine the maxima and minima of the function f(x) = 2x3 - 21x2 + 36x - 20 . Also, find the maximum and minimum values of f(x).
If `f'(x)=k(cosx-sinx), f'(0)=3 " and " f(pi/2)=15`, find f(x).
Find the maximum and minimum value, if any, of the following function given by g(x) = x3 + 1.
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
g(x) = x3 − 3x
What is the maximum value of the function sin x + cos x?
A rectangular sheet of tin 45 cm by 24 cm is to be made into a box without top, by cutting off square from each corner and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is the maximum possible?
Find the maximum area of an isosceles triangle inscribed in the ellipse `x^2/ a^2 + y^2/b^2 = 1` with its vertex at one end of the major axis.
A window is in the form of a rectangle surmounted by a semicircular opening. The total perimeter of the window is 10 m. Find the dimensions of the window to admit maximum light through the whole opening
Show that the cone of the greatest volume which can be inscribed in a given sphere has an altitude equal to \[ \frac{2}{3} \] of the diameter of the sphere.
A rod of 108 meters long is bent to form a rectangle. Find its dimensions if the area is maximum. Let x be the length and y be the breadth of the rectangle.
Find the maximum and minimum of the following functions : f(x) = x3 – 9x2 + 24x
Divide the number 30 into two parts such that their product is maximum.
An open cylindrical tank whose base is a circle is to be constructed of metal sheet so as to contain a volume of `pia^3`cu cm of water. Find the dimensions so that the quantity of the metal sheet required is minimum.
Divide the number 20 into two parts such that their product is maximum.
Find the local maximum and local minimum value of f(x) = x3 − 3x2 − 24x + 5
A rectangular sheet of paper has it area 24 sq. Meters. The margin at the top and the bottom are 75 cm each and the sides 50 cm each. What are the dimensions of the paper if the area of the printed space is maximum?
Divide the number 20 into two parts such that their product is maximum
If f(x) = 3x3 - 9x2 - 27x + 15, then the maximum value of f(x) is _______.
Let f have second derivative at c such that f′(c) = 0 and f"(c) > 0, then c is a point of ______.
Find the points of local maxima, local minima and the points of inflection of the function f(x) = x5 – 5x4 + 5x3 – 1. Also find the corresponding local maximum and local minimum values.
A metal box with a square base and vertical sides is to contain 1024 cm3. The material for the top and bottom costs Rs 5/cm2 and the material for the sides costs Rs 2.50/cm2. Find the least cost of the box.
Maximum slope of the curve y = –x3 + 3x2 + 9x – 27 is ______.
Find both the maximum and minimum values respectively of 3x4 - 8x3 + 12x2 - 48x + 1 on the interval [1, 4].
Let f(x) = 1 + 2x2 + 22x4 + …… + 210x20. Then f (x) has ____________.
A ball is thrown upward at a speed of 28 meter per second. What is the speed of ball one second before reaching maximum height? (Given that g= 10 meter per second2)
If p(x) be a polynomial of degree three that has a local maximum value 8 at x = 1 and a local minimum value 4 at x = 2; then p(0) is equal to ______.
The maximum distance from origin of a point on the curve x = `a sin t - b sin((at)/b)`, y = `a cos t - b cos((at)/b)`, both a, b > 0 is ______.
If f(x) = `1/(4x^2 + 2x + 1); x ∈ R`, then find the maximum value of f(x).
A right circular cylinder is to be made so that the sum of the radius and height is 6 metres. Find the maximum volume of the cylinder.
