Advertisements
Advertisements
प्रश्न
A metal box with a square base and vertical sides is to contain 1024 cm3. The material for the top and bottom costs Rs 5/cm2 and the material for the sides costs Rs 2.50/cm2. Find the least cost of the box.
उत्तर
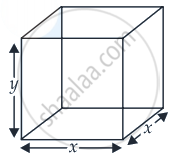
Let x be the side of the square base and y be the length of the vertical sides.
Area of the base and bottom = 2x2 cm2
∴ Cost of the material required = ₹ 5 × 2x2
= ₹ 10x2
Area of the 4 sides = 4xy cm2
∴ Cost of the material for the four sides
= ₹ 2.50 x 4xy
= ₹ 10xy
Total cost C = 10x2 + 10xy .....(i)
New volume of the box = x × x × y
⇒ 1024 = x2y
∴ y = `1024/x^2` ....(ii)
Putting the value of y in equation (i) we get
C = `10x^2 + 10x xx 1024/x^2`
⇒ C = `10x^2 + 10240/x`
Differentiating both sides w.r.t. x, we get
`"dC"/"dx" = 20x - 10240/x^2` ....(iii)
For local maxima and local minima `"dC"/"dx"` = 0
`20 - 102400/x^2` = 0
⇒ 20x3 – 10240 = 0
⇒ x3 = 512
⇒ x = 8 cm
Now from equation (ii)
y = `10240/(8)^2`
= `10240/64`
= 16 cm
∴ Cost of material used C = 10x2 + 10xy
= 10 × 8 × 8 + 10 × 8 × 16
= 640 + 1280
= 1920
Now differentiating equation (iii) we get
`("d"^2"C")/("dx"^2) = 20 + 20480/x^3`
Put x = 8
= `20 + 20480/(8)^3`
= `20 + 20480/512`
= 20 + 40 = 60 > 0 minima
Hence, the required cost is ₹ 1920 which is the minimum.
APPEARS IN
संबंधित प्रश्न
Find the maximum and minimum value, if any, of the function given by f(x) = |x + 2| − 1.
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
g(x) = x3 − 3x
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
`h(x) = sinx + cosx, 0 < x < pi/2`
Find the maximum value of 2x3 − 24x + 107 in the interval [1, 3]. Find the maximum value of the same function in [−3, −1].
A square piece of tin of side 18 cm is to made into a box without a top by cutting a square from each corner and folding up the flaps to form the box. What should be the side of the square to be cut off so that the volume of the box is the maximum possible?
For all real values of x, the minimum value of `(1 - x + x^2)/(1+x+x^2)` is ______.
Find the maximum area of an isosceles triangle inscribed in the ellipse `x^2/ a^2 + y^2/b^2 = 1` with its vertex at one end of the major axis.
Find the absolute maximum and minimum values of the function f given by f (x) = cos2 x + sin x, x ∈ [0, π].
A metal box with a square base and vertical sides is to contain 1024 cm3. The material for the top and bottom costs Rs 5 per cm2 and the material for the sides costs Rs 2.50 per cm2. Find the least cost of the box
An open tank with a square base and vertical sides is to be constructed from a metal sheet so as to hold a given quantity of water. Show that the cost of material will be least when the depth of the tank is half of its width. If the cost is to be borne by nearby settled lower-income families, for whom water will be provided, what kind of value is hidden in this question?
Find the maximum and minimum of the following functions : f(x) = `logx/x`
Divide the number 20 into two parts such that their product is maximum.
If z = ax + by; a, b > 0 subject to x ≤ 2, y ≤ 2, x + y ≥ 3, x ≥ 0, y ≥ 0 has minimum value at (2, 1) only, then ______.
The two parts of 120 for which the sum of double of first and square of second part is minimum, are ______.
Show that the function f(x) = 4x3 – 18x2 + 27x – 7 has neither maxima nor minima.
If the sum of the lengths of the hypotenuse and a side of a right-angled triangle is given, show that the area of the triangle is maximum when the angle between them is `pi/3`
An open box with square base is to be made of a given quantity of cardboard of area c2. Show that the maximum volume of the box is `"c"^3/(6sqrt(3))` cubic units
Maximum slope of the curve y = –x3 + 3x2 + 9x – 27 is ______.
The maximum value of `["x"("x" − 1) + 1]^(1/3)`, 0 ≤ x ≤ 1 is:
Find the local minimum value of the function f(x) `= "sin"^4" x + cos"^4 "x", 0 < "x" < pi/2`
For all real values of `x`, the minimum value of `(1 - x + x^2)/(1 + x + x^2)`
The maximum value of `[x(x - 1) + 1]^(2/3), 0 ≤ x ≤ 1` is
The greatest value of the function f(x) = `tan^-1x - 1/2logx` in `[1/sqrt(3), sqrt(3)]` is ______.
The maximum distance from origin of a point on the curve x = `a sin t - b sin((at)/b)`, y = `a cos t - b cos((at)/b)`, both a, b > 0 is ______.
A rectangle with one side lying along the x-axis is to be inscribed in the closed region of the xy plane bounded by the lines y = 0, y = 3x and y = 30 – 2x. The largest area of such a rectangle is ______.
Check whether the function f : R `rightarrow` R defined by f(x) = x3 + x, has any critical point/s or not ? If yes, then find the point/s.
