Advertisements
Advertisements
प्रश्न
If the sum of the lengths of the hypotenuse and a side of a right-angled triangle is given, show that the area of the triangle is maximum when the angle between them is `pi/3`
उत्तर
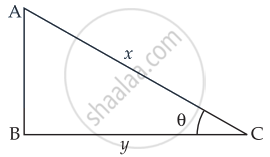
Let ΔABC be the right angled triangle in which ∠B = 90°
Let AC = x, BC = y
∴ AB = `sqrt(x^2 - y^2)`
∠ACB = θ
Let Z = x + y ....(Given)
Now area of ΔABC, A = `1/2 xx "AB" xx "BC"`
⇒ A = `1/2 y * sqrt(x^2 - y^2)`
⇒ A = `1/2 y * sqrt(("Z" - y)^2 - y^2)`
Squaring both sides, we get
⇒ A2 = `1/4 y^2 [("Z" - y)^2 - y^2]`
⇒ A2 = `1/4 y^2 ["Z"^2 + y^2 - 2"Z" y - y^2]`
⇒ P = `1/4 y^2 ["Z"^2 - 2"Z"y]`
⇒ P = `1/4 [y^2"Z"^2 - 2"Z"y^3]` ....[A2 = P]
Differentiating both sides w.r.t. y we get
`"dP"/"dy" = 1/4 [2y"Z"^2 - 6"Z"y^2]` .....(i)
For local maxima and local minima,
`"dP"/"dy"` = 0
∴ `1/4 (2y"Z"^2 - 6"Z"y^2)` = 0
⇒ `(2y"Z")/4 ("Z" - 3y)` = 0
⇒ yZ(Z – 3y) = 0
⇒ yZ ≠ 0 .....(∵ y ≠ 0 and Z ≠ 0)
⇒ Z – 3y = 0
⇒ y = `"Z"/3`
⇒ y = `(x + y)/3` .....(∵ Z = x + y)
⇒ 3y = x + y
⇒ 3y – y = x
⇒ 2y = x
⇒ `y/x = 1/2`
⇒ cos θ = `1/2`
∴ θ = `pi/3`
Differentiating eq. (i) w.r.t. y,
We have `("d"^2"P")/("dy"^2) = 1/4 [2"Z"^2 - 12"Z"y]`
`("d"^2"P")/("dy"^2)` at y = `"Z"/3 = 1/4 [2"Z"^2 - 12"Z" * "Z"/3]`
= `1/4 [2"Z"^2 - 4"Z"^2]`
= `(-"Z"^2)/2 < 0`
Hence, the area of the given triangle is maximum when the angle between its hypotenuse and a side is `pi/3`.
APPEARS IN
संबंधित प्रश्न
Find the maximum and minimum value, if any, of the following function given by g(x) = x3 + 1.
Find the maximum and minimum value, if any, of the following function given by f(x) = |sin 4x + 3|
Find the local maxima and local minima, if any, of the following functions. Find also the local maximum and the local minimum values, as the case may be:
`f(x) = xsqrt(1-x), x > 0`
Find the absolute maximum value and the absolute minimum value of the following function in the given interval:
`f(x) = 4x - 1/x x^2, x in [-2 ,9/2]`
Find the maximum and minimum values of x + sin 2x on [0, 2π].
Find two numbers whose sum is 24 and whose product is as large as possible.
Show that semi-vertical angle of right circular cone of given surface area and maximum volume is `Sin^(-1) (1/3).`
A window is in the form of a rectangle surmounted by a semicircular opening. The total perimeter of the window is 10 m. Find the dimensions of the window to admit maximum light through the whole opening
Find the absolute maximum and minimum values of the function f given by f (x) = cos2 x + sin x, x ∈ [0, π].
Show that the cone of the greatest volume which can be inscribed in a given sphere has an altitude equal to \[ \frac{2}{3} \] of the diameter of the sphere.
Show that a cylinder of a given volume, which is open at the top, has minimum total surface area when its height is equal to the radius of its base.
Find the point on the straight line 2x+3y = 6, which is closest to the origin.
Find the maximum and minimum of the following functions : y = 5x3 + 2x2 – 3x.
Find the maximum and minimum of the following functions : f(x) = x3 – 9x2 + 24x
A wire of length 36 metres is bent in the form of a rectangle. Find its dimensions if the area of the rectangle is maximum.
The function f(x) = x log x is minimum at x = ______.
A rod of 108 m long is bent to form a rectangle. Find it’s dimensions when it’s area is maximum.
If z = ax + by; a, b > 0 subject to x ≤ 2, y ≤ 2, x + y ≥ 3, x ≥ 0, y ≥ 0 has minimum value at (2, 1) only, then ______.
If f(x) = `x + 1/x, x ne 0`, then local maximum and x minimum values of function f are respectively.
Twenty meters of wire is available for fencing off a flowerbed in the form of a circular sector. Then the maximum area (in sq. m) of the flower-bed, is ______
Find the points of local maxima, local minima and the points of inflection of the function f(x) = x5 – 5x4 + 5x3 – 1. Also find the corresponding local maximum and local minimum values.
If x is real, the minimum value of x2 – 8x + 17 is ______.
The curves y = 4x2 + 2x – 8 and y = x3 – x + 13 touch each other at the point ______.
The combined resistance R of two resistors R1 and R2 (R1, R2 > 0) is given by `1/"R" = 1/"R"_1 + 1/"R"_2`. If R1 + R2 = C (a constant), then maximum resistance R is obtained if ____________.
Let f: R → R be a function defined by f(x) = (x – 3)n1(x – 5)n2, n1, n2 ∈ N. Then, which of the following is NOT true?
A running track of 440 m is to be laid out enclosing a football field. The football field is in the shape of a rectangle with a semi-circle at each end. If the area of the rectangular portion is to be maximum,then find the length of its sides. Also calculate the area of the football field.
A right circular cylinder is to be made so that the sum of the radius and height is 6 metres. Find the maximum volume of the cylinder.
A box with a square base is to have an open top. The surface area of box is 147 sq. cm. What should be its dimensions in order that the volume is largest?
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
f(x) `= x sqrt(1 - x), 0 < x < 1`
