Advertisements
Advertisements
प्रश्न
If the sum of the lengths of the hypotenuse and a side of a right-angled triangle is given, show that the area of the triangle is maximum when the angle between them is `pi/3`
उत्तर
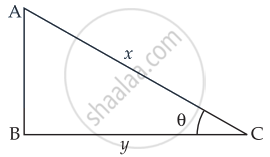
Let ΔABC be the right angled triangle in which ∠B = 90°
Let AC = x, BC = y
∴ AB = `sqrt(x^2 - y^2)`
∠ACB = θ
Let Z = x + y ....(Given)
Now area of ΔABC, A = `1/2 xx "AB" xx "BC"`
⇒ A = `1/2 y * sqrt(x^2 - y^2)`
⇒ A = `1/2 y * sqrt(("Z" - y)^2 - y^2)`
Squaring both sides, we get
⇒ A2 = `1/4 y^2 [("Z" - y)^2 - y^2]`
⇒ A2 = `1/4 y^2 ["Z"^2 + y^2 - 2"Z" y - y^2]`
⇒ P = `1/4 y^2 ["Z"^2 - 2"Z"y]`
⇒ P = `1/4 [y^2"Z"^2 - 2"Z"y^3]` ....[A2 = P]
Differentiating both sides w.r.t. y we get
`"dP"/"dy" = 1/4 [2y"Z"^2 - 6"Z"y^2]` .....(i)
For local maxima and local minima,
`"dP"/"dy"` = 0
∴ `1/4 (2y"Z"^2 - 6"Z"y^2)` = 0
⇒ `(2y"Z")/4 ("Z" - 3y)` = 0
⇒ yZ(Z – 3y) = 0
⇒ yZ ≠ 0 .....(∵ y ≠ 0 and Z ≠ 0)
⇒ Z – 3y = 0
⇒ y = `"Z"/3`
⇒ y = `(x + y)/3` .....(∵ Z = x + y)
⇒ 3y = x + y
⇒ 3y – y = x
⇒ 2y = x
⇒ `y/x = 1/2`
⇒ cos θ = `1/2`
∴ θ = `pi/3`
Differentiating eq. (i) w.r.t. y,
We have `("d"^2"P")/("dy"^2) = 1/4 [2"Z"^2 - 12"Z"y]`
`("d"^2"P")/("dy"^2)` at y = `"Z"/3 = 1/4 [2"Z"^2 - 12"Z" * "Z"/3]`
= `1/4 [2"Z"^2 - 4"Z"^2]`
= `(-"Z"^2)/2 < 0`
Hence, the area of the given triangle is maximum when the angle between its hypotenuse and a side is `pi/3`.
APPEARS IN
संबंधित प्रश्न
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
`h(x) = sinx + cosx, 0 < x < pi/2`
Find the maximum value of 2x3 − 24x + 107 in the interval [1, 3]. Find the maximum value of the same function in [−3, −1].
It is given that at x = 1, the function x4− 62x2 + ax + 9 attains its maximum value, on the interval [0, 2]. Find the value of a.
Find two positive numbers x and y such that their sum is 35 and the product x2y5 is a maximum.
Show that of all the rectangles inscribed in a given fixed circle, the square has the maximum area.
Find the absolute maximum and minimum values of the function f given by f (x) = cos2 x + sin x, x ∈ [0, π].
Show that the surface area of a closed cuboid with square base and given volume is minimum, when it is a cube.
An open tank with a square base and vertical sides is to be constructed from a metal sheet so as to hold a given quantity of water. Show that the cost of material will be least when the depth of the tank is half of its width. If the cost is to be borne by nearby settled lower-income families, for whom water will be provided, what kind of value is hidden in this question?
Find the maximum and minimum of the following functions : f(x) = 2x3 – 21x2 + 36x – 20
The perimeter of a triangle is 10 cm. If one of the side is 4 cm. What are the other two sides of the triangle for its maximum area?
The profit function P(x) of a firm, selling x items per day is given by P(x) = (150 – x)x – 1625 . Find the number of items the firm should manufacture to get maximum profit. Find the maximum profit.
Solve the following:
Find the maximum and minimum values of the function f(x) = cos2x + sinx.
Determine the maximum and minimum value of the following function.
f(x) = x log x
Determine the maximum and minimum value of the following function.
f(x) = `x^2 + 16/x`
Examine the function for maxima and minima f(x) = x3 - 9x2 + 24x
Let f have second derivative at c such that f′(c) = 0 and f"(c) > 0, then c is a point of ______.
Find the points of local maxima, local minima and the points of inflection of the function f(x) = x5 – 5x4 + 5x3 – 1. Also find the corresponding local maximum and local minimum values.
Find the points of local maxima and local minima respectively for the function f(x) = sin 2x - x, where `-pi/2 le "x" le pi/2`
Find the maximum profit that a company can make, if the profit function is given by P(x) = 41 + 24x – 18x2.
The function `f(x) = x^3 - 6x^2 + 9x + 25` has
Let P(h, k) be a point on the curve y = x2 + 7x + 2, nearest to the line, y = 3x – 3. Then the equation of the normal to the curve at P is ______.
If p(x) be a polynomial of degree three that has a local maximum value 8 at x = 1 and a local minimum value 4 at x = 2; then p(0) is equal to ______.
Let x and y be real numbers satisfying the equation x2 – 4x + y2 + 3 = 0. If the maximum and minimum values of x2 + y2 are a and b respectively. Then the numerical value of a – b is ______.
Let f(x) = (x – a)ng(x) , where g(n)(a) ≠ 0; n = 0, 1, 2, 3.... then ______.
A cone of maximum volume is inscribed in a given sphere. Then the ratio of the height of the cone to the diameter of the sphere is ______.
The maximum value of f(x) = `logx/x (x ≠ 0, x ≠ 1)` is ______.
Find two numbers whose sum is 15 and when the square of one number multiplied by the cube of the other is maximum.
Find the maximum and the minimum values of the function f(x) = x2ex.
