Advertisements
Advertisements
प्रश्न
The perimeter of a triangle is 10 cm. If one of the side is 4 cm. What are the other two sides of the triangle for its maximum area?
उत्तर
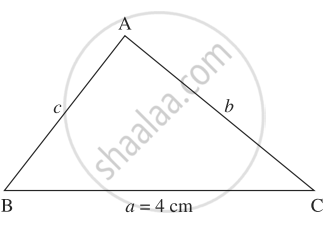
Let ABC be the triangle such that the side BC = a = 4 cm. Also, the perimeter of the triangle is 10 cm.
i.e. a + b + c = 10
∴ 2s = 10
∴ s = 5
Also, 4 + b + c = 10
∴ b + c = 6
∴ b = 6 – c
Let Δ be the area of the trangle.
Then Δ = `sqrt(s(s - a)(s - b)(s - c)`
= `sqrt(5(5 - 4)(5 - 6 + c)(5 - c)`
= `sqrt(5(c - 1)(5 - c)`
∴ Δ2 = 5(c – 1)(5 – c)
= 5(5c – c2 – 5 + c)
∴ Δ2 = 5(– c2 + 6c – 5)
Differentiable both sides ww.r.t. c, we get
`2Δ(dΔ)/(dc) = 5d/"dc"(-c^2 ++ 6c - 5)`
= 5 (– 2c + 6 x 1 – 0)
= 5 (– 2c + 6)
∴ `(dΔ)/"dc" = (5(-c + 3))/Δ`
and
`(d^2Δ)/(dc^2) = 5d/"dc"((-c + 3)/Δ)`
= `5.(Δd/"dc"(– c + 3) – ( – c + 3)(dΔ)/"dc")/Δ^2`
= `5.(Δ(– 1 + 0) – ( – c + 3)(dΔ)/"dc")/Δ^2`
= `5/Δ^2(-Δ - (c + 3)(dΔ)/"dc")`
= `(-5)/Δ^2[Δ + (c + 3)(dΔ)/"dc"]`
For maximum Δ, `(dΔ)/"dc"` = 0
∴ `(5( - c + 3))/Δ` = 0
∴ – c + 3 = 0 ...[∵ Δ ≠ 0]
∴ c = 3
If c = 3,
Δ = `sqrt(5(3 - 1)(5 - 3)`
= `2sqrt(5)`
∴ `((d^2Δ)/(dc^2))_("at" c = 3)`
= `(-5)/(4 xx 5)[2sqrt(5) + (3 + 3)(0)]`
= `sqrt(5)/(2) < 0`
∴ by the second derivative test, Δ is maximum when c= 3.
When c = 3, b = 6 – c = 6 – 3 = 3
Hence, the area of the triangle is maximum when the other two sides are 3cm and 3cm.
APPEARS IN
संबंधित प्रश्न
Find the approximate value of cos (89°, 30'). [Given is: 1° = 0.0175°C]
An open box is to be made out of a piece of a square card board of sides 18 cms by cutting off equal squares from the comers and turning up the sides. Find the maximum volume of the box.
Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is `(4r)/3`. Also find maximum volume in terms of volume of the sphere
Find the maximum and minimum value, if any, of the following function given by f(x) = (2x − 1)2 + 3.
Find the maximum and minimum value, if any, of the following function given by f(x) = 9x2 + 12x + 2
Find the maximum and minimum value, if any, of the function given by f(x) = |x + 2| − 1.
Find the maximum and minimum value, if any, of the following function given by h(x) = sin(2x) + 5.
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
f(x) = x2
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
g(x) = x3 − 3x
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
f(x) = sinx − cos x, 0 < x < 2π
Find the local maxima and local minima, if any, of the following functions. Find also the local maximum and the local minimum values, as the case may be:
`f(x) = xsqrt(1-x), x > 0`
Prove that the following function do not have maxima or minima:
f(x) = ex
At what points in the interval [0, 2π], does the function sin 2x attain its maximum value?
What is the maximum value of the function sin x + cos x?
It is given that at x = 1, the function x4− 62x2 + ax + 9 attains its maximum value, on the interval [0, 2]. Find the value of a.
Of all the closed cylindrical cans (right circular), of a given volume of 100 cubic centimetres, find the dimensions of the can which has the minimum surface area?
Show that the right circular cone of least curved surface and given volume has an altitude equal to `sqrt2` time the radius of the base.
Show that semi-vertical angle of right circular cone of given surface area and maximum volume is `Sin^(-1) (1/3).`
The maximum value of `[x(x −1) +1]^(1/3)` , 0 ≤ x ≤ 1 is ______.
Find the points at which the function f given by f (x) = (x – 2)4 (x + 1)3 has
- local maxima
- local minima
- point of inflexion
Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is `(4r)/3.`
A metal box with a square base and vertical sides is to contain 1024 cm3. The material for the top and bottom costs Rs 5 per cm2 and the material for the sides costs Rs 2.50 per cm2. Find the least cost of the box
An open tank with a square base and vertical sides is to be constructed from a metal sheet so as to hold a given quantity of water. Show that the cost of material will be least when the depth of the tank is half of its width. If the cost is to be borne by nearby settled lower-income families, for whom water will be provided, what kind of value is hidden in this question?
Show that the cone of the greatest volume which can be inscribed in a given sphere has an altitude equal to \[ \frac{2}{3} \] of the diameter of the sphere.
Show that a cylinder of a given volume, which is open at the top, has minimum total surface area when its height is equal to the radius of its base.
The volume of a closed rectangular metal box with a square base is 4096 cm3. The cost of polishing the outer surface of the box is Rs. 4 per cm2. Find the dimensions of the box for the minimum cost of polishing it.
Find the maximum and minimum of the following functions : f(x) = `x^2 + (16)/x^2`
Find the maximum and minimum of the following functions : f(x) = x log x
Divide the number 20 into two parts such that sum of their squares is minimum.
A ball is thrown in the air. Its height at any time t is given by h = 3 + 14t – 5t2. Find the maximum height it can reach.
Show that among rectangles of given area, the square has least perimeter.
Solve the following : An open box with a square base is to be made out of given quantity of sheet of area a2. Show that the maximum volume of the box is `a^3/(6sqrt(3)`.
Solve the following : Show that of all rectangles inscribed in a given circle, the square has the maximum area.
Solve the following : Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is `(4r)/(3)`.
Solve the following : Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is `(2"R")/sqrt(3)`. Also, find the maximum volume.
Determine the maximum and minimum value of the following function.
f(x) = x log x
If f(x) = x.log.x then its maximum value is ______.
Find the local maximum and local minimum value of f(x) = x3 − 3x2 − 24x + 5
A rod of 108 m long is bent to form a rectangle. Find it’s dimensions when it’s area is maximum.
By completing the following activity, examine the function f(x) = x3 – 9x2 + 24x for maxima and minima
Solution: f(x) = x3 – 9x2 + 24x
∴ f'(x) = `square`
∴ f''(x) = `square`
For extreme values, f'(x) = 0, we get
x = `square` or `square`
∴ f''`(square)` = – 6 < 0
∴ f(x) is maximum at x = 2.
∴ Maximum value = `square`
∴ f''`(square)` = 6 > 0
∴ f(x) is maximum at x = 4.
∴ Minimum value = `square`
If f(x) = px5 + qx4 + 5x3 - 10 has local maximum and minimum at x = 1 and x = 3 respectively then (p, q) = ______.
The maximum volume of a right circular cylinder if the sum of its radius and height is 6 m is ______.
If f(x) = `x + 1/x, x ne 0`, then local maximum and x minimum values of function f are respectively.
The function y = 1 + sin x is maximum, when x = ______
The maximum value of function x3 - 15x2 + 72x + 19 in the interval [1, 10] is ______.
The minimum value of the function f(x) = 13 - 14x + 9x2 is ______
Find all the points of local maxima and local minima of the function f(x) = `- 3/4 x^4 - 8x^3 - 45/2 x^2 + 105`
Find the points of local maxima, local minima and the points of inflection of the function f(x) = x5 – 5x4 + 5x3 – 1. Also find the corresponding local maximum and local minimum values.
A telephone company in a town has 500 subscribers on its list and collects fixed charges of Rs 300/- per subscriber per year. The company proposes to increase the annual subscription and it is believed that for every increase of Re 1/- one subscriber will discontinue the service. Find what increase will bring maximum profit?
AB is a diameter of a circle and C is any point on the circle. Show that the area of ∆ABC is maximum, when it is isosceles.
The sum of the surface areas of a rectangular parallelopiped with sides x, 2x and `x/3` and a sphere is given to be constant. Prove that the sum of their volumes is minimum, if x is equal to three times the radius of the sphere. Also find the minimum value of the sum of their volumes.
If x is real, the minimum value of x2 – 8x + 17 is ______.
The smallest value of the polynomial x3 – 18x2 + 96x in [0, 9] is ______.
The maximum value of `["x"("x" − 1) + 1]^(1/3)`, 0 ≤ x ≤ 1 is:
If y = x3 + x2 + x + 1, then y ____________.
Find the height of the cylinder of maximum volume that can be inscribed in a sphere of radius a.
Find the area of the largest isosceles triangle having a perimeter of 18 meters.
The function `f(x) = x^3 - 6x^2 + 9x + 25` has
Read the following passage and answer the questions given below.
|
In an elliptical sport field the authority wants to design a rectangular soccer field with the maximum possible area. The sport field is given by the graph of `x^2/a^2 + y^2/b^2` = 1. |
- If the length and the breadth of the rectangular field be 2x and 2y respectively, then find the area function in terms of x.
- Find the critical point of the function.
- Use First derivative Test to find the length 2x and width 2y of the soccer field (in terms of a and b) that maximize its area.
OR
Use Second Derivative Test to find the length 2x and width 2y of the soccer field (in terms of a and b) that maximize its area.
A wire of length 36 m is cut into two pieces, one of the pieces is bent to form a square and the other is bent to form a circle. If the sum of the areas of the two figures is minimum, and the circumference of the circle is k (meter), then `(4/π + 1)`k is equal to ______.
The function g(x) = `(f(x))/x`, x ≠ 0 has an extreme value when ______.
Let f(x) = (x – a)ng(x) , where g(n)(a) ≠ 0; n = 0, 1, 2, 3.... then ______.
The lateral edge of a regular rectangular pyramid is 'a' cm long. The lateral edge makes an angle a. with the plane of the base. The value of a for which the volume of the pyramid is greatest, is ______.
The maximum distance from origin of a point on the curve x = `a sin t - b sin((at)/b)`, y = `a cos t - b cos((at)/b)`, both a, b > 0 is ______.
The volume of the greatest cylinder which can be inscribed in a cone of height 30 cm and semi-vertical angle 30° is ______.
A rod AB of length 16 cm. rests between the wall AD and a smooth peg, 1 cm from the wall and makes an angle θ with the horizontal. The value of θ for which the height of G, the midpoint of the rod above the peg is minimum, is ______.
Sum of two numbers is 5. If the sum of the cubes of these numbers is least, then find the sum of the squares of these numbers.
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
f(x) `= x sqrt(1 - x), 0 < x < 1`
Mrs. Roy designs a window in her son’s study room so that the room gets maximum sunlight. She designs the window in the shape of a rectangle surmounted by an equilateral triangle. If the perimeter of the window is 12 m, find the dimensions of the window that will admit maximum sunlight into the room.
Sumit has bought a closed cylindrical dustbin. The radius of the dustbin is ‘r' cm and height is 'h’ cm. It has a volume of 20π cm3.
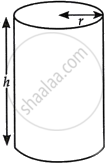
- Express ‘h’ in terms of ‘r’, using the given volume.
- Prove that the total surface area of the dustbin is `2πr^2 + (40π)/r`
- Sumit wants to paint the dustbin. The cost of painting the base and top of the dustbin is ₹ 2 per cm2 and the cost of painting the curved side is ₹ 25 per cm2. Find the total cost in terms of ‘r’, for painting the outer surface of the dustbin including the base and top.
- Calculate the minimum cost for painting the dustbin.

