Advertisements
Advertisements
प्रश्न
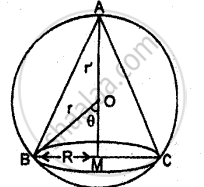
Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is `(4r)/3.`
Advertisements
उत्तर
Let the radius of the sphere = r
Radius of cone = R
Height of the cone = AM
= OA + OM
= r + r cos θ
= r(1 + cosθ)
where ∠BOM = θ
BC = diameter of the base of the cone
∴ Radius of cone = r sin θ
Volume of cone V = `1/3 pi (r sin theta)^2 xx r (1 + cos theta)` ....`[because "volume of cone" = 1/3 pir^2 h]`
`= 1/3 pir^3 sin^2 theta (1 + cos theta)`
On differentiating,
`(dV)/(d theta) = 1/3 pir^3 [2 sin theta cos theta (1 + cos theta) + sin^2 theta (- sin theta)]`
`= 1/3 pir^3 [2 sin theta cos theta (1 + cos theta) - sin^3 theta]`
`= 1/3 pir^3 sin theta [2 cos theta (1 + cos theta) - sin^2 theta]`
`= 1/3 pir^3 sin theta [2 cos theta + 2 cos^2 theta - 1+ cos^2 theta]`
`= 1/3 pir^3 sin theta [3 cos^2 theta + 2 cos theta - 1]`
`= 1/3 pir^3 sin theta (cos theta + 1)(3 cos theta - 1)`
For maximum and minimum, `(dV)/(d theta) = 0`
⇒ cos θ ≠ - 1
⇒ θ ≠ π
∴ (3 cos θ - 1) = 0
⇒ `cos theta = 1/3`
In the interval `(0, pi/2)` cos θ is decreasing, cos θ increases as θ decreases and decreases as θ increases.
⇒ at cos θ = `1/3`
The sign of `(dV)/(d theta)` changes from positive to negative as θ passes through this point.
Hence V is highest at this point.
Height of the cone = `r (1 + cos theta) = r(1 + 1/3)`
`= r xx 4/3`
= `(4r)/3`
APPEARS IN
संबंधित प्रश्न
Examine the maxima and minima of the function f(x) = 2x3 - 21x2 + 36x - 20 . Also, find the maximum and minimum values of f(x).
Show that the height of the cylinder of maximum volume, that can be inscribed in a sphere of radius R is `(2R)/sqrt3.` Also, find the maximum volume.
An open box is to be made out of a piece of a square card board of sides 18 cms by cutting off equal squares from the comers and turning up the sides. Find the maximum volume of the box.
A telephone company in a town has 5000 subscribers on its list and collects fixed rent charges of Rs.3,000 per year from each subscriber. The company proposes to increase annual rent and it is believed that for every increase of one rupee in the rent, one subscriber will be discontinued. Find what increased annual rent will bring the maximum annual income to the company.
Find the maximum and minimum value, if any, of the following function given by f(x) = −(x − 1)2 + 10
Find the maximum and minimum value, if any, of the following function given by h(x) = sin(2x) + 5.
Find the maximum and minimum value, if any, of the following function given by h(x) = x + 1, x ∈ (−1, 1)
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
`g(x) = x/2 + 2/x, x > 0`
Find the maximum profit that a company can make, if the profit function is given by p(x) = 41 − 72x − 18x2.
What is the maximum value of the function sin x + cos x?
A rectangular sheet of tin 45 cm by 24 cm is to be made into a box without top, by cutting off square from each corner and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is the maximum possible?
Show that of all the rectangles inscribed in a given fixed circle, the square has the maximum area.
Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is `tan^(-1) sqrt(2)`
The point on the curve x2 = 2y which is nearest to the point (0, 5) is ______.
A point on the hypotenuse of a triangle is at distance a and b from the sides of the triangle.
Show that the minimum length of the hypotenuse is `(a^(2/3) + b^(2/3))^(3/2).`
Show that the cone of the greatest volume which can be inscribed in a given sphere has an altitude equal to \[ \frac{2}{3} \] of the diameter of the sphere.
Find the maximum and minimum of the following functions : y = 5x3 + 2x2 – 3x.
Find the maximum and minimum of the following functions : f(x) = 2x3 – 21x2 + 36x – 20
A ball is thrown in the air. Its height at any time t is given by h = 3 + 14t – 5t2. Find the maximum height it can reach.
Find the largest size of a rectangle that can be inscribed in a semicircle of radius 1 unit, so that two vertices lie on the diameter.
Show that among rectangles of given area, the square has least perimeter.
Solve the following : An open box with a square base is to be made out of given quantity of sheet of area a2. Show that the maximum volume of the box is `a^3/(6sqrt(3)`.
Solve the following : A window is in the form of a rectangle surmounted by a semicircle. If the perimeter be 30 m, find the dimensions so that the greatest possible amount of light may be admitted.
A metal wire of 36 cm length is bent to form a rectangle. Find its dimensions when its area is maximum.
Find the local maximum and local minimum value of f(x) = x3 − 3x2 − 24x + 5
If f(x) = px5 + qx4 + 5x3 - 10 has local maximum and minimum at x = 1 and x = 3 respectively then (p, q) = ______.
The sum of two non-zero numbers is 6. The minimum value of the sum of their reciprocals is ______.
Find all the points of local maxima and local minima of the function f(x) = `- 3/4 x^4 - 8x^3 - 45/2 x^2 + 105`
If the sum of the lengths of the hypotenuse and a side of a right-angled triangle is given, show that the area of the triangle is maximum when the angle between them is `pi/3`
The sum of the surface areas of a rectangular parallelopiped with sides x, 2x and `x/3` and a sphere is given to be constant. Prove that the sum of their volumes is minimum, if x is equal to three times the radius of the sphere. Also find the minimum value of the sum of their volumes.
The smallest value of the polynomial x3 – 18x2 + 96x in [0, 9] is ______.
Find the area of the largest isosceles triangle having a perimeter of 18 meters.
Range of projectile will be maximum when angle of projectile is
For all real values of `x`, the minimum value of `(1 - x + x^2)/(1 + x + x^2)`
The maximum value of `[x(x - 1) + 1]^(2/3), 0 ≤ x ≤ 1` is
The minimum value of α for which the equation `4/sinx + 1/(1 - sinx)` = α has at least one solution in `(0, π/2)` is ______.
The function g(x) = `(f(x))/x`, x ≠ 0 has an extreme value when ______.
The rectangle has area of 50 cm2. Complete the following activity to find its dimensions for least perimeter.
Solution: Let x cm and y cm be the length and breadth of a rectangle.
Then its area is xy = 50
∴ `y =50/x`
Perimeter of rectangle `=2(x+y)=2(x+50/x)`
Let f(x) `=2(x+50/x)`
Then f'(x) = `square` and f''(x) = `square`
Now,f'(x) = 0, if x = `square`
But x is not negative.
∴ `x = root(5)(2) "and" f^('')(root(5)(2))=square>0`
∴ by the second derivative test f is minimum at x = `root(5)(2)`
When x = `root(5)(2),y=50/root(5)(2)=root(5)(2)`
∴ `x=root(5)(2) "cm" , y = root(5)(2) "cm"`
Hence, rectangle is a square of side `root(5)(2) "cm"`
Find the maximum and the minimum values of the function f(x) = x2ex.
Divide the number 100 into two parts so that the sum of their squares is minimum.
