Advertisements
Advertisements
प्रश्न
Solve the following : Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is `(2"R")/sqrt(3)`. Also, find the maximum volume.
उत्तर
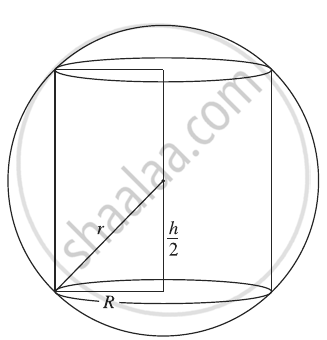
Let R be the radius and h be the height of the cylinder which is inscribed in a sphere of radius r cm.
Then from the figure,
`"R"^2 + (h/2)^2` = r2
∴ R2 = `r^2 - h^2/(4)` ...(1)
Let V be the volume of the cylinder.
Then V = πR2h
= `pi(r^2 - h^2/(4))h` ...[By (1)]
= `pi(r^2 - h^3/(4))`
∴ `"dV"/"dh" = pid/"dh"(r^2h - h^3/(4))`
= `pi(r^2 xx 1 - 1/4 xx 3h^2)`
= `pi(r^2 - 3/4h^2)`
and
`(d^2V)/("dh"^2) = pid/"dh"(r^2 - 3/4h^2)`
= `pi(0 - 3/4 xx 2h)`
= `-(3)/(2)pih`
Now, `"dV"/"dh" = 0 "gives", pi(r^2 - 3/4h^2)` = 0
∴ `r^2 - 3/4h^2` = 0
∴ `(3)/(4)h^2` = r2
∴ h2 = `(4r^2)/(3)`
∴ h = `(2r)/sqrt(3)` ...[∵ h > 0]
and
`((d^2V)/(dh^2))_("at" h = (2r)/sqrt(3)`
= `-(3)/(2)pi xx (2r)/sqrt(3) < 0`
∴ V is maximum at h = `(2r)/sqrt(3)`
If h = `(2r)/sqrt(3)`, then from (1)
R2 = `r^2 - (1)/(4) xx (4r^2)/(3) = (2r^2)/(3)`
∴ volumeof the largest cylinder
= `pi xx (2r^2)/(3) xx (2r)/sqrt(3) = (4pir^3)/(3sqrt(3)`cu cm.
Hence, the volume of the largest cylinder inscribed in a sphere of radius 'r' cm = `(4R^3)/(3sqrt(3)`cu cm.
APPEARS IN
संबंधित प्रश्न
If the sum of lengths of hypotenuse and a side of a right angled triangle is given, show that area of triangle is maximum, when the angle between them is π/3.
Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is `(4r)/3`. Also find maximum volume in terms of volume of the sphere
Find the maximum and minimum value, if any, of the following function given by f(x) = −(x − 1)2 + 10
Find the maximum and minimum value, if any, of the function given by f(x) = |x + 2| − 1.
Find the maximum and minimum value, if any, of the following function given by h(x) = x + 1, x ∈ (−1, 1)
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
f(x) = x2
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
f(x) = sinx − cos x, 0 < x < 2π
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
f(x) = x3 − 6x2 + 9x + 15
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
`g(x) = x/2 + 2/x, x > 0`
Prove that the following function do not have maxima or minima:
g(x) = logx
Find the absolute maximum value and the absolute minimum value of the following function in the given interval:
`f(x) =x^3, x in [-2,2]`
Find the absolute maximum value and the absolute minimum value of the following function in the given interval:
f (x) = sin x + cos x , x ∈ [0, π]
Find both the maximum value and the minimum value of 3x4 − 8x3 + 12x2 − 48x + 25 on the interval [0, 3].
Find the maximum value of 2x3 − 24x + 107 in the interval [1, 3]. Find the maximum value of the same function in [−3, −1].
It is given that at x = 1, the function x4− 62x2 + ax + 9 attains its maximum value, on the interval [0, 2]. Find the value of a.
Find two positive numbers whose sum is 16 and the sum of whose cubes is minimum.
A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the length of the two pieces so that the combined area of the square and the circle is minimum?
Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is `tan^(-1) sqrt(2)`
The point on the curve x2 = 2y which is nearest to the point (0, 5) is ______.
For all real values of x, the minimum value of `(1 - x + x^2)/(1+x+x^2)` is ______.
A metal box with a square base and vertical sides is to contain 1024 cm3. The material for the top and bottom costs Rs 5 per cm2 and the material for the sides costs Rs 2.50 per cm2. Find the least cost of the box
Show that a cylinder of a given volume, which is open at the top, has minimum total surface area when its height is equal to the radius of its base.
A rod of 108 meters long is bent to form a rectangle. Find its dimensions if the area is maximum. Let x be the length and y be the breadth of the rectangle.
A rectangle is inscribed in a semicircle of radius r with one of its sides on the diameter of the semicircle. Find the dimensions of the rectangle to get the maximum area. Also, find the maximum area.
Find the maximum and minimum of the following functions : f(x) = `x^2 + (16)/x^2`
Divide the number 20 into two parts such that sum of their squares is minimum.
A wire of length 36 metres is bent in the form of a rectangle. Find its dimensions if the area of the rectangle is maximum.
The perimeter of a triangle is 10 cm. If one of the side is 4 cm. What are the other two sides of the triangle for its maximum area?
A box with a square base is to have an open top. The surface area of the box is 192 sq cm. What should be its dimensions in order that the volume is largest?
Show that among rectangles of given area, the square has least perimeter.
Solve the following : Show that of all rectangles inscribed in a given circle, the square has the maximum area.
Solve the following : Show that a closed right circular cylinder of given surface area has maximum volume if its height equals the diameter of its base.
Solve the following:
A rectangular sheet of paper of fixed perimeter with the sides having their lengths in the ratio 8 : 15 converted into an open rectangular box by folding after removing the squares of equal area from all corners. If the total area of the removed squares is 100, the resulting box has maximum volume. Find the lengths of the rectangular sheet of paper.
Solve the following : Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is `(4r)/(3)`.
Solve the following:
Find the maximum and minimum values of the function f(x) = cos2x + sinx.
Determine the maximum and minimum value of the following function.
f(x) = 2x3 – 21x2 + 36x – 20
A rod of 108 m long is bent to form a rectangle. Find it’s dimensions when it’s area is maximum.
The maximum value of function x3 - 15x2 + 72x + 19 in the interval [1, 10] is ______.
The two parts of 120 for which the sum of double of first and square of second part is minimum, are ______.
The sum of two non-zero numbers is 6. The minimum value of the sum of their reciprocals is ______.
Show that the function f(x) = 4x3 – 18x2 + 27x – 7 has neither maxima nor minima.
Find the points of local maxima, local minima and the points of inflection of the function f(x) = x5 – 5x4 + 5x3 – 1. Also find the corresponding local maximum and local minimum values.
A metal box with a square base and vertical sides is to contain 1024 cm3. The material for the top and bottom costs Rs 5/cm2 and the material for the sides costs Rs 2.50/cm2. Find the least cost of the box.
Maximum slope of the curve y = –x3 + 3x2 + 9x – 27 is ______.
The curves y = 4x2 + 2x – 8 and y = x3 – x + 13 touch each other at the point ______.
If y = x3 + x2 + x + 1, then y ____________.
Find both the maximum and minimum values respectively of 3x4 - 8x3 + 12x2 - 48x + 1 on the interval [1, 4].
Find the height of the cylinder of maximum volume that can be inscribed in a sphere of radius a.
Find the volume of the largest cylinder that can be inscribed in a sphere of radius r cm.
The distance of that point on y = x4 + 3x2 + 2x which is nearest to the line y = 2x - 1 is ____________.
The function `"f"("x") = "x" + 4/"x"` has ____________.
The combined resistance R of two resistors R1 and R2 (R1, R2 > 0) is given by `1/"R" = 1/"R"_1 + 1/"R"_2`. If R1 + R2 = C (a constant), then maximum resistance R is obtained if ____________.
Let f(x) = 1 + 2x2 + 22x4 + …… + 210x20. Then f (x) has ____________.
The function `f(x) = x^3 - 6x^2 + 9x + 25` has
For all real values of `x`, the minimum value of `(1 - x + x^2)/(1 + x + x^2)`
The maximum value of `[x(x - 1) + 1]^(2/3), 0 ≤ x ≤ 1` is
Divide 20 into two ports, so that their product is maximum.
Read the following passage and answer the questions given below.
|
|
- Is the function differentiable in the interval (0, 12)? Justify your answer.
- If 6 is the critical point of the function, then find the value of the constant m.
- Find the intervals in which the function is strictly increasing/strictly decreasing.
OR
Find the points of local maximum/local minimum, if any, in the interval (0, 12) as well as the points of absolute maximum/absolute minimum in the interval [0, 12]. Also, find the corresponding local maximum/local minimum and the absolute ‘maximum/absolute minimum values of the function.
Read the following passage and answer the questions given below.
|
In an elliptical sport field the authority wants to design a rectangular soccer field with the maximum possible area. The sport field is given by the graph of `x^2/a^2 + y^2/b^2` = 1. |
- If the length and the breadth of the rectangular field be 2x and 2y respectively, then find the area function in terms of x.
- Find the critical point of the function.
- Use First derivative Test to find the length 2x and width 2y of the soccer field (in terms of a and b) that maximize its area.
OR
Use Second Derivative Test to find the length 2x and width 2y of the soccer field (in terms of a and b) that maximize its area.
The range of a ∈ R for which the function f(x) = `(4a - 3)(x + log_e5) + 2(a - 7)cot(x/2)sin^2(x/2), x ≠ 2nπ, n∈N` has critical points, is ______.
If p(x) be a polynomial of degree three that has a local maximum value 8 at x = 1 and a local minimum value 4 at x = 2; then p(0) is equal to ______.
If the point (1, 3) serves as the point of inflection of the curve y = ax3 + bx2 then the value of 'a ' and 'b' are ______.
The set of values of p for which the points of extremum of the function f(x) = x3 – 3px2 + 3(p2 – 1)x + 1 lie in the interval (–2, 4), is ______.
The lateral edge of a regular rectangular pyramid is 'a' cm long. The lateral edge makes an angle a. with the plane of the base. The value of a for which the volume of the pyramid is greatest, is ______.
The minimum value of 2sinx + 2cosx is ______.
A rectangle with one side lying along the x-axis is to be inscribed in the closed region of the xy plane bounded by the lines y = 0, y = 3x and y = 30 – 2x. The largest area of such a rectangle is ______.
A metal wire of 36 cm long is bent to form a rectangle. Find its dimensions when its area is maximum.
Find the maximum and the minimum values of the function f(x) = x2ex.
A running track of 440 m is to be laid out enclosing a football field. The football field is in the shape of a rectangle with a semi-circle at each end. If the area of the rectangular portion is to be maximum,then find the length of its sides. Also calculate the area of the football field.
If x + y = 8, then the maximum value of x2y is ______.
Determine the minimum value of the function.
f(x) = 2x3 – 21x2 + 36x – 20
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
f(x) `= x sqrt(1 - x), 0 < x < 1`
Mrs. Roy designs a window in her son’s study room so that the room gets maximum sunlight. She designs the window in the shape of a rectangle surmounted by an equilateral triangle. If the perimeter of the window is 12 m, find the dimensions of the window that will admit maximum sunlight into the room.