Advertisements
Advertisements
प्रश्न
A rectangle is inscribed in a semicircle of radius r with one of its sides on the diameter of the semicircle. Find the dimensions of the rectangle to get the maximum area. Also, find the maximum area.
उत्तर
Breadth = x, length = `2sqrt("r"^2-"x"^2)`
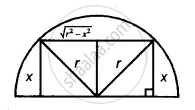
A = `2"x"sqrt("r"^2-"x"^2)`
`"dA"/"dx" = 2 sqrt("r"^2-"x"^2) + (2"x")/(2sqrt("r"^2-"x"^2) )(-2"x")`
`("d"^2"A")/("dx"^2) = 2/(2sqrt("r"^2-"x"^2))( -2"x") - (4"x")/sqrt("r"^2-"x"^2) +(2"x"^2)/(2("r"^2-"x"^2)^(3/2)) (-2"x")<0`
Hence, area is maximum
Point of maxima is given by : `"dA"/"dx" = 0`
⇒ `(2("r"^2 -"x"^2 -"x"^2))/sqrt("r"^2-"x"^2) = 0`
⇒ `"x"="r"/sqrt2`
∴ Breadth =`"r"/sqrt2,` length =`sqrt2"r"`
Maximum area = r2
APPEARS IN
संबंधित प्रश्न
If the sum of lengths of hypotenuse and a side of a right angled triangle is given, show that area of triangle is maximum, when the angle between them is π/3.
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
`h(x) = sinx + cosx, 0 < x < pi/2`
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
f(x) = sinx − cos x, 0 < x < 2π
Prove that the following function do not have maxima or minima:
f(x) = ex
Prove that the following function do not have maxima or minima:
h(x) = x3 + x2 + x + 1
Find the maximum profit that a company can make, if the profit function is given by p(x) = 41 − 72x − 18x2.
What is the maximum value of the function sin x + cos x?
Show that semi-vertical angle of right circular cone of given surface area and maximum volume is `Sin^(-1) (1/3).`
Show that a cylinder of a given volume, which is open at the top, has minimum total surface area when its height is equal to the radius of its base.
The volume of a closed rectangular metal box with a square base is 4096 cm3. The cost of polishing the outer surface of the box is Rs. 4 per cm2. Find the dimensions of the box for the minimum cost of polishing it.
Show that the height of a cylinder, which is open at the top, having a given surface area and greatest volume, is equal to the radius of its base.
The perimeter of a triangle is 10 cm. If one of the side is 4 cm. What are the other two sides of the triangle for its maximum area?
Determine the maximum and minimum value of the following function.
f(x) = x log x
If f(x) = x.log.x then its maximum value is ______.
Examine the function for maxima and minima f(x) = x3 - 9x2 + 24x
Max value of z equals 3x + 2y subject to x + y ≤ 3, x ≤ 2, -2x + y ≤ 1, x ≥ 0, y ≥ 0 is ______
If f(x) = `x + 1/x, x ne 0`, then local maximum and x minimum values of function f are respectively.
The maximum value of function x3 - 15x2 + 72x + 19 in the interval [1, 10] is ______.
The two parts of 120 for which the sum of double of first and square of second part is minimum, are ______.
If y = x3 + x2 + x + 1, then y ____________.
Find the height of the cylinder of maximum volume that can be inscribed in a sphere of radius a.
Find the volume of the largest cylinder that can be inscribed in a sphere of radius r cm.
The combined resistance R of two resistors R1 and R2 (R1, R2 > 0) is given by `1/"R" = 1/"R"_1 + 1/"R"_2`. If R1 + R2 = C (a constant), then maximum resistance R is obtained if ____________.
Divide 20 into two ports, so that their product is maximum.
A function f(x) is maximum at x = a when f'(a) > 0.
The maximum value of z = 6x + 8y subject to constraints 2x + y ≤ 30, x + 2y ≤ 24 and x ≥ 0, y ≥ 0 is ______.
The maximum value of f(x) = `logx/x (x ≠ 0, x ≠ 1)` is ______.
Sum of two numbers is 5. If the sum of the cubes of these numbers is least, then find the sum of the squares of these numbers.
A right circular cylinder is to be made so that the sum of the radius and height is 6 metres. Find the maximum volume of the cylinder.
