Advertisements
Advertisements
Question
A rectangle is inscribed in a semicircle of radius r with one of its sides on the diameter of the semicircle. Find the dimensions of the rectangle to get the maximum area. Also, find the maximum area.
Solution
Breadth = x, length = `2sqrt("r"^2-"x"^2)`
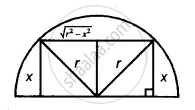
A = `2"x"sqrt("r"^2-"x"^2)`
`"dA"/"dx" = 2 sqrt("r"^2-"x"^2) + (2"x")/(2sqrt("r"^2-"x"^2) )(-2"x")`
`("d"^2"A")/("dx"^2) = 2/(2sqrt("r"^2-"x"^2))( -2"x") - (4"x")/sqrt("r"^2-"x"^2) +(2"x"^2)/(2("r"^2-"x"^2)^(3/2)) (-2"x")<0`
Hence, area is maximum
Point of maxima is given by : `"dA"/"dx" = 0`
⇒ `(2("r"^2 -"x"^2 -"x"^2))/sqrt("r"^2-"x"^2) = 0`
⇒ `"x"="r"/sqrt2`
∴ Breadth =`"r"/sqrt2,` length =`sqrt2"r"`
Maximum area = r2
APPEARS IN
RELATED QUESTIONS
Find the maximum and minimum value, if any, of the following function given by h(x) = x + 1, x ∈ (−1, 1)
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
f(x) = x2
Find the absolute maximum value and the absolute minimum value of the following function in the given interval:
`f(x) = 4x - 1/x x^2, x in [-2 ,9/2]`
Find two positive numbers x and y such that x + y = 60 and xy3 is maximum.
Show that the right circular cylinder of given surface and maximum volume is such that is heights is equal to the diameter of the base.
Of all the closed cylindrical cans (right circular), of a given volume of 100 cubic centimetres, find the dimensions of the can which has the minimum surface area?
Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is `tan^(-1) sqrt(2)`
Find the point on the straight line 2x+3y = 6, which is closest to the origin.
Find the maximum and minimum of the following functions : f(x) = `x^2 + (16)/x^2`
Divide the number 20 into two parts such that sum of their squares is minimum.
A ball is thrown in the air. Its height at any time t is given by h = 3 + 14t – 5t2. Find the maximum height it can reach.
Show that among rectangles of given area, the square has least perimeter.
Choose the correct option from the given alternatives :
If f(x) = `(x^2 - 1)/(x^2 + 1)`, for every real x, then the minimum value of f is ______.
Solve the following : Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is `(4r)/(3)`.
The total cost of producing x units is ₹ (x2 + 60x + 50) and the price is ₹ (180 − x) per unit. For what units is the profit maximum?
If f(x) = x.log.x then its maximum value is ______.
By completing the following activity, examine the function f(x) = x3 – 9x2 + 24x for maxima and minima
Solution: f(x) = x3 – 9x2 + 24x
∴ f'(x) = `square`
∴ f''(x) = `square`
For extreme values, f'(x) = 0, we get
x = `square` or `square`
∴ f''`(square)` = – 6 < 0
∴ f(x) is maximum at x = 2.
∴ Maximum value = `square`
∴ f''`(square)` = 6 > 0
∴ f(x) is maximum at x = 4.
∴ Minimum value = `square`
If f(x) = 3x3 - 9x2 - 27x + 15, then the maximum value of f(x) is _______.
The maximum and minimum values for the function f(x) = 4x3 - 6x2 on [-1, 2] are ______
The two parts of 120 for which the sum of double of first and square of second part is minimum, are ______.
An open box with square base is to be made of a given quantity of cardboard of area c2. Show that the maximum volume of the box is `"c"^3/(6sqrt(3))` cubic units
Find the points of local maxima and local minima respectively for the function f(x) = sin 2x - x, where `-pi/2 le "x" le pi/2`
The point on the curve `x^2 = 2y` which is nearest to the point (0, 5) is
For all real values of `x`, the minimum value of `(1 - x + x^2)/(1 + x + x^2)`
If S1 and S2 are respectively the sets of local minimum and local maximum points of the function. f(x) = 9x4 + 12x3 – 36x2 + 25, x ∈ R, then ______.
The sum of all the local minimum values of the twice differentiable function f : R `rightarrow` R defined by
f(x) = `x^3 - 3x^2 - (3f^('')(2))/2 x + f^('')(1)`
The maximum distance from origin of a point on the curve x = `a sin t - b sin((at)/b)`, y = `a cos t - b cos((at)/b)`, both a, b > 0 is ______.
If f(x) = `1/(4x^2 + 2x + 1); x ∈ R`, then find the maximum value of f(x).
A running track of 440 m is to be laid out enclosing a football field. The football field is in the shape of a rectangle with a semi-circle at each end. If the area of the rectangular portion is to be maximum,then find the length of its sides. Also calculate the area of the football field.
