Advertisements
Advertisements
Question
An open box with square base is to be made of a given quantity of cardboard of area c2. Show that the maximum volume of the box is `"c"^3/(6sqrt(3))` cubic units
Solution
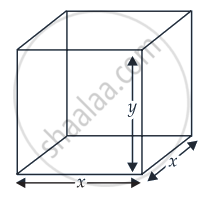
Let x be the length of the side of the square base of the cubical open box and y be its height.
∴ Surface area of the open box
c2 = x2 + 4xy
⇒ y = `("c"^2 - x^2)/(4x)` ....(i)
Now volume of the box, V = x × x × y
⇒ V = x2y
⇒ V = `x^2(("c"^2 - x^2)/(4x))`
⇒ V = `1/4 ("c"^2x - x^3)`
Differentiating both sides w.r.t. x, we get
`"dv"/"dx" = 1/4 ("c"^2 - 3x^2)` ....(ii)
For local maxima and local minima, `"dV"/"dx"` = 0
∴ `1/4 ("c"^2 - 3x^2)` = 0
⇒ c2 – 3x2 = 0
⇒ x2 = `"c"^2/3`
∴ x = `sqrt("c"^2/3) = "c"/sqrt(3)`
Now again differentiating equation (ii) w.r.t. x, we get
`("d"^2"V")/("dx"^2) = 1/4 (- 6x)`
= `(-3)/2 * "c"/sqrt(3) < 0` ...(maxima)
Volume of the cubical box (V) = x2y
= `x^2(("c"^2 - x^2)/4x)`
= `"c"/sqrt(3)[("c"^2 - "c"^2/3)/4]`
= `"c"/sqrt(3) xx (2"c"^2)/(3 xx 4)`
= `"c"^3/(6sqrt(3))`
Hence, the maximum volume of the open box is `"c"^3/(6sqrt(3))` cubic units.
APPEARS IN
RELATED QUESTIONS
If `f'(x)=k(cosx-sinx), f'(0)=3 " and " f(pi/2)=15`, find f(x).
Show that the height of the cylinder of maximum volume, that can be inscribed in a sphere of radius R is `(2R)/sqrt3.` Also, find the maximum volume.
If the sum of lengths of hypotenuse and a side of a right angled triangle is given, show that area of triangle is maximum, when the angle between them is π/3.
Find the maximum and minimum value, if any, of the following function given by g(x) = − |x + 1| + 3.
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
f(x) = sinx − cos x, 0 < x < 2π
Prove that the following function do not have maxima or minima:
h(x) = x3 + x2 + x + 1
Find the absolute maximum value and the absolute minimum value of the following function in the given interval:
`f(x) =x^3, x in [-2,2]`
A square piece of tin of side 18 cm is to made into a box without a top by cutting a square from each corner and folding up the flaps to form the box. What should be the side of the square to be cut off so that the volume of the box is the maximum possible?
Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is `tan^(-1) sqrt(2)`
A window is in the form of a rectangle surmounted by a semicircular opening. The total perimeter of the window is 10 m. Find the dimensions of the window to admit maximum light through the whole opening
A point on the hypotenuse of a triangle is at distance a and b from the sides of the triangle.
Show that the minimum length of the hypotenuse is `(a^(2/3) + b^(2/3))^(3/2).`
Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is `(4r)/3.`
Find the point on the straight line 2x+3y = 6, which is closest to the origin.
Find the maximum and minimum of the following functions : f(x) = `logx/x`
Solve the following : An open box with a square base is to be made out of given quantity of sheet of area a2. Show that the maximum volume of the box is `a^3/(6sqrt(3)`.
Solve the following : A window is in the form of a rectangle surmounted by a semicircle. If the perimeter be 30 m, find the dimensions so that the greatest possible amount of light may be admitted.
The total cost of producing x units is ₹ (x2 + 60x + 50) and the price is ₹ (180 − x) per unit. For what units is the profit maximum?
State whether the following statement is True or False:
An absolute maximum must occur at a critical point or at an end point.
A wire of length 120 cm is bent in the form of a rectangle. Find its dimensions if the area of the rectangle is maximum
By completing the following activity, examine the function f(x) = x3 – 9x2 + 24x for maxima and minima
Solution: f(x) = x3 – 9x2 + 24x
∴ f'(x) = `square`
∴ f''(x) = `square`
For extreme values, f'(x) = 0, we get
x = `square` or `square`
∴ f''`(square)` = – 6 < 0
∴ f(x) is maximum at x = 2.
∴ Maximum value = `square`
∴ f''`(square)` = 6 > 0
∴ f(x) is maximum at x = 4.
∴ Minimum value = `square`
AB is a diameter of a circle and C is any point on the circle. Show that the area of ∆ABC is maximum, when it is isosceles.
If x is real, the minimum value of x2 – 8x + 17 is ______.
If y `= "ax - b"/(("x" - 1)("x" - 4))` has a turning point P(2, -1), then find the value of a and b respectively.
For all real values of `x`, the minimum value of `(1 - x + x^2)/(1 + x + x^2)`
A wire of length 22 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into an equilateral triangle. Then, the length of the side of the equilateral triangle, so that the combined area of the square and the equilateral triangle is minimum, is ______.
The greatest value of the function f(x) = `tan^-1x - 1/2logx` in `[1/sqrt(3), sqrt(3)]` is ______.
The sum of all the local minimum values of the twice differentiable function f : R `rightarrow` R defined by
f(x) = `x^3 - 3x^2 - (3f^('')(2))/2 x + f^('')(1)`
A rod AB of length 16 cm. rests between the wall AD and a smooth peg, 1 cm from the wall and makes an angle θ with the horizontal. The value of θ for which the height of G, the midpoint of the rod above the peg is minimum, is ______.
Find two numbers whose sum is 15 and when the square of one number multiplied by the cube of the other is maximum.
Sum of two numbers is 5. If the sum of the cubes of these numbers is least, then find the sum of the squares of these numbers.
