Advertisements
Advertisements
Question
Show that the height of the cylinder of maximum volume, that can be inscribed in a sphere of radius R is `(2R)/sqrt3.` Also, find the maximum volume.
Advertisements
Solution 1
Given that the radius of the sphere is R,.
Let r and h be the radius and height of the inscribed cylinder, respectively.
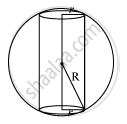
From the given figure, we have `h=2sqrt(R^2-r^2)`
The volume (V) of the cylinder is given by,
`V=pir^2h=2pir^2sqrt(R^2-r^2)`
`therefore (dV)/(dr)=4pirsqrt(R^2-r^2)+(2pir^2(-2r))/(2sqrt(R^2-r^2))`
`=(4pirR^2-6pir^3)/sqrt(R^2-r^2)`
for maxima or minima, `(dV)/(dr) =0 `
`(4pirR^2-6pir^3)=0`
`r^2=(2R^2)/3`
Now `,(d^2V)/(dr^2)=(sqrt(R^2-r^2)(4piR^2-18pir^2)-(4piR^2-6pir^3)(-2r)/(2sqrt(R^2-r^2)))/(R^2-r^2)`
`=((R^2-r^2)(4piR^2-18pir^2)-r(4piR^2-6pir^3))/(R^2-r^2)^(3/2)`
`=(4piR^4-22pir^2R^2+12pir^4+4pir^2R^2)/(R^2-r^2)^(3/2)`
Now, it can be observed that when `r^2=(2RR62)/3,(d^2V)/(dr^2)<0`
The volume is the maximum when `r^2=(2R^2)/3`
Maximum volume = V = `pih((4R^2 - h^2)/4)`
`h = 2R/sqrt3`
`V_(max) = pi xx 2R/sqrt3 ((4R^2 - 4R^2/3)/4)`
` = (2piR)/sqrt3 . (2R^2)/3 = (4piR^3)/(3sqrt3)` cubic units
Hence, the volume of the cylinder is at its maximum when the height of the cylinder is `(2R)/3`
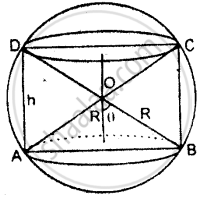
Solution 2
Let the radius of the sphere, OA = R
makes an angle θ with the axis of the cylinder.
Radius of cylinder = R sin θ
Height of cylinder = 2R cos θ
∴ Volume of cylinder = πr2h
V = π (R sin θ)2 × 2 R cos θ
= 2πR3 sin2 θ cos θ
On differentiating with respect to θ,
`(dV)/(d theta) = 2piR^2 [sin^2 theta (- sin theta) + cos theta * 2 sin theta cos theta]`
= 2πR3 [- sin3 θ + 2 cos2 θ sin θ]
= 2πR3 sin θ (2 cos2 θ - sin2 θ)
= 2πR3 sin θ (2 cos2 θ - 1 + cos2 θ)
= 2πR3 sin θ (3 cos2 θ - 1)
For maximum and minimum, `(dV)/(d theta) = 0`
⇒ 2πR3 sin θ (3 cos2 θ - 1) = 0
3 cos2 θ - 1 = 0 या `cos^2 theta = 1/3`
`therefore cos theta = 1/sqrt3`
At `cos theta = 1/sqrt3` the sign of `(dV)/(d theta)` changes from positive to negative when θ passes through cos θ = `1/sqrt3`.
V is maximum at `=> cos theta = 1/sqrt3`.
Height = 2 R cos θ = 2R `* 1/sqrt3 = (2R)/3`
∴ Maximum volume of cylinder = 2πR3 sin2 θ cos θ
`= 2piR^3 (sqrt2/sqrt3)^2 1/sqrt3 ...[because cos theta = 1/sqrt3, sin theta = sqrt2/sqrt3]`
`= 2piR^3 xx 2/3 * 1/sqrt3`
`= (4 piR^3)/(3 sqrt3)` square unit.
APPEARS IN
RELATED QUESTIONS
If the sum of lengths of hypotenuse and a side of a right angled triangle is given, show that area of triangle is maximum, when the angle between them is π/3.
Find the maximum and minimum value, if any, of the following function given by f(x) = 9x2 + 12x + 2
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
`g(x) = 1/(x^2 + 2)`
Prove that the following function do not have maxima or minima:
h(x) = x3 + x2 + x + 1
What is the maximum value of the function sin x + cos x?
The point on the curve x2 = 2y which is nearest to the point (0, 5) is ______.
Show that the surface area of a closed cuboid with square base and given volume is minimum, when it is a cube.
The volume of a closed rectangular metal box with a square base is 4096 cm3. The cost of polishing the outer surface of the box is Rs. 4 per cm2. Find the dimensions of the box for the minimum cost of polishing it.
Find the point on the straight line 2x+3y = 6, which is closest to the origin.
Show that the height of a cylinder, which is open at the top, having a given surface area and greatest volume, is equal to the radius of its base.
The perimeter of a triangle is 10 cm. If one of the side is 4 cm. What are the other two sides of the triangle for its maximum area?
Show that the height of a closed right circular cylinder of given volume and least surface area is equal to its diameter.
Solve the following : An open box with a square base is to be made out of given quantity of sheet of area a2. Show that the maximum volume of the box is `a^3/(6sqrt(3)`.
Solve the following:
A wire of length l is cut into two parts. One part is bent into a circle and the other into a square. Show that the sum of the areas of the circle and the square is the least, if the radius of the circle is half of the side of the square.
Divide the number 20 into two parts such that their product is maximum.
Find the local maximum and local minimum value of f(x) = x3 − 3x2 − 24x + 5
Divide the number 20 into two parts such that their product is maximum
A rod of 108 m long is bent to form a rectangle. Find it’s dimensions when it’s area is maximum.
By completing the following activity, examine the function f(x) = x3 – 9x2 + 24x for maxima and minima
Solution: f(x) = x3 – 9x2 + 24x
∴ f'(x) = `square`
∴ f''(x) = `square`
For extreme values, f'(x) = 0, we get
x = `square` or `square`
∴ f''`(square)` = – 6 < 0
∴ f(x) is maximum at x = 2.
∴ Maximum value = `square`
∴ f''`(square)` = 6 > 0
∴ f(x) is maximum at x = 4.
∴ Minimum value = `square`
Twenty meters of wire is available for fencing off a flowerbed in the form of a circular sector. Then the maximum area (in sq. m) of the flower-bed, is ______
The sum of two non-zero numbers is 6. The minimum value of the sum of their reciprocals is ______.
The sum of the surface areas of a rectangular parallelopiped with sides x, 2x and `x/3` and a sphere is given to be constant. Prove that the sum of their volumes is minimum, if x is equal to three times the radius of the sphere. Also find the minimum value of the sum of their volumes.
If x is real, the minimum value of x2 – 8x + 17 is ______.
The smallest value of the polynomial x3 – 18x2 + 96x in [0, 9] is ______.
Find all the points of local maxima and local minima of the function f(x) = (x - 1)3 (x + 1)2
Find the maximum profit that a company can make, if the profit function is given by P(x) = 41 + 24x – 18x2.
The coordinates of the point on the parabola y2 = 8x which is at minimum distance from the circle x2 + (y + 6)2 = 1 are ____________.
The maximum value of the function f(x) = `logx/x` is ______.
A wire of length 22 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into an equilateral triangle. Then, the length of the side of the equilateral triangle, so that the combined area of the square and the equilateral triangle is minimum, is ______.
The range of a ∈ R for which the function f(x) = `(4a - 3)(x + log_e5) + 2(a - 7)cot(x/2)sin^2(x/2), x ≠ 2nπ, n∈N` has critical points, is ______.
Let P(h, k) be a point on the curve y = x2 + 7x + 2, nearest to the line, y = 3x – 3. Then the equation of the normal to the curve at P is ______.
Let x and y be real numbers satisfying the equation x2 – 4x + y2 + 3 = 0. If the maximum and minimum values of x2 + y2 are a and b respectively. Then the numerical value of a – b is ______.
The lateral edge of a regular rectangular pyramid is 'a' cm long. The lateral edge makes an angle a. with the plane of the base. The value of a for which the volume of the pyramid is greatest, is ______.
Check whether the function f : R `rightarrow` R defined by f(x) = x3 + x, has any critical point/s or not ? If yes, then find the point/s.
A running track of 440 m is to be laid out enclosing a football field. The football field is in the shape of a rectangle with a semi-circle at each end. If the area of the rectangular portion is to be maximum,then find the length of its sides. Also calculate the area of the football field.
Divide the number 100 into two parts so that the sum of their squares is minimum.
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
f(x) `= x sqrt(1 - x), 0 < x < 1`
Mrs. Roy designs a window in her son’s study room so that the room gets maximum sunlight. She designs the window in the shape of a rectangle surmounted by an equilateral triangle. If the perimeter of the window is 12 m, find the dimensions of the window that will admit maximum sunlight into the room.
