Question

Show that the height of the cylinder of maximum volume, that can be inscribed in a sphere of radius R is `(2R)/sqrt3.`  Also, find the maximum volume.

Answer 1

Given that the radius of the sphere is R,.

Let r and h be the radius and height of the inscribed cylinder, respectively.

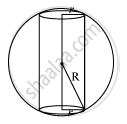
From the given figure, we have `h=2sqrt(R^2-r^2)`

The volume (V) of the cylinder is given by,

`V=pir^2h=2pir^2sqrt(R^2-r^2)`

`therefore (dV)/(dr)=4pirsqrt(R^2-r^2)+(2pir^2(-2r))/(2sqrt(R^2-r^2))`

`=(4pirR^2-6pir^3)/sqrt(R^2-r^2)`

for maxima or minima, `(dV)/(dr) =0 `

`(4pirR^2-6pir^3)=0`

`r^2=(2R^2)/3`

Now `,(d^2V)/(dr^2)=(sqrt(R^2-r^2)(4piR^2-18pir^2)-(4piR^2-6pir^3)(-2r)/(2sqrt(R^2-r^2)))/(R^2-r^2)`

`=((R^2-r^2)(4piR^2-18pir^2)-r(4piR^2-6pir^3))/(R^2-r^2)^(3/2)`

`=(4piR^4-22pir^2R^2+12pir^4+4pir^2R^2)/(R^2-r^2)^(3/2)`

Now, it can be observed that when `r^2=(2RR62)/3,(d^2V)/(dr^2)<0`

The volume is the maximum when `r^2=(2R^2)/3`

Maximum volume = V = `pih((4R^2 - h^2)/4)`
            `h = 2R/sqrt3`

`V_(max) = pi xx 2R/sqrt3 ((4R^2 - 4R^2/3)/4)`

` = (2piR)/sqrt3 . (2R^2)/3 = (4piR^3)/(3sqrt3)` cubic units

Hence, the volume of the cylinder is at its maximum when the height of the cylinder is `(2R)/3`

Answer 2

Let the radius of the sphere, OA = R

makes an angle θ with the axis of the cylinder.

Radius of cylinder = R sin θ

Height of cylinder = 2R cos θ

∴ Volume of cylinder = πr²h

V = π (R sin θ)² × 2 R cos θ

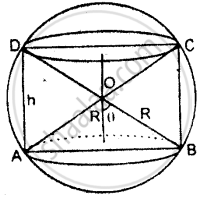
= 2πR³ sin² θ cos θ

On differentiating with respect to θ,

`(dV)/(d theta) = 2piR^2 [sin^2 theta (- sin theta) + cos theta * 2 sin theta cos theta]`

= 2πR³ [- sin³ θ + 2 cos² θ sin θ]

= 2πR³ sin θ (2 cos² θ - sin² θ)

= 2πR³ sin θ (2 cos² θ - 1 + cos² θ)

= 2πR³ sin θ (3 cos² θ - 1)

For maximum and minimum, `(dV)/(d theta) = 0`

⇒ 2πR³ sin θ (3 cos² θ - 1) = 0

3 cos² θ - 1 = 0  या  `cos^2 theta = 1/3`

`therefore cos theta = 1/sqrt3`

At `cos theta = 1/sqrt3` the sign of `(dV)/(d theta)` changes from positive to negative when θ passes through cos θ  = `1/sqrt3`.

V is maximum at `=> cos theta = 1/sqrt3`.

Height = 2 R cos θ = 2R `* 1/sqrt3 = (2R)/3`

∴ Maximum volume of cylinder = 2πR³ sin² θ cos θ

`= 2piR^3 (sqrt2/sqrt3)^2 1/sqrt3                   ...[because cos theta = 1/sqrt3, sin theta = sqrt2/sqrt3]`

`= 2piR^3 xx 2/3 * 1/sqrt3`

`= (4 piR^3)/(3 sqrt3)` square unit.