Advertisements
Advertisements
प्रश्न
An open box with square base is to be made of a given quantity of cardboard of area c2. Show that the maximum volume of the box is `"c"^3/(6sqrt(3))` cubic units
उत्तर
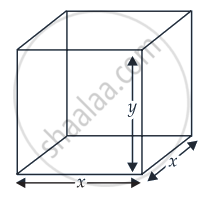
Let x be the length of the side of the square base of the cubical open box and y be its height.
∴ Surface area of the open box
c2 = x2 + 4xy
⇒ y = `("c"^2 - x^2)/(4x)` ....(i)
Now volume of the box, V = x × x × y
⇒ V = x2y
⇒ V = `x^2(("c"^2 - x^2)/(4x))`
⇒ V = `1/4 ("c"^2x - x^3)`
Differentiating both sides w.r.t. x, we get
`"dv"/"dx" = 1/4 ("c"^2 - 3x^2)` ....(ii)
For local maxima and local minima, `"dV"/"dx"` = 0
∴ `1/4 ("c"^2 - 3x^2)` = 0
⇒ c2 – 3x2 = 0
⇒ x2 = `"c"^2/3`
∴ x = `sqrt("c"^2/3) = "c"/sqrt(3)`
Now again differentiating equation (ii) w.r.t. x, we get
`("d"^2"V")/("dx"^2) = 1/4 (- 6x)`
= `(-3)/2 * "c"/sqrt(3) < 0` ...(maxima)
Volume of the cubical box (V) = x2y
= `x^2(("c"^2 - x^2)/4x)`
= `"c"/sqrt(3)[("c"^2 - "c"^2/3)/4]`
= `"c"/sqrt(3) xx (2"c"^2)/(3 xx 4)`
= `"c"^3/(6sqrt(3))`
Hence, the maximum volume of the open box is `"c"^3/(6sqrt(3))` cubic units.
APPEARS IN
संबंधित प्रश्न
If the sum of lengths of hypotenuse and a side of a right angled triangle is given, show that area of triangle is maximum, when the angle between them is π/3.
Find the maximum and minimum value, if any, of the following function given by h(x) = sin(2x) + 5.
Find the maximum and minimum value, if any, of the following function given by f(x) = |sin 4x + 3|
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
`h(x) = sinx + cosx, 0 < x < pi/2`
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
`g(x) = 1/(x^2 + 2)`
Prove that the following function do not have maxima or minima:
g(x) = logx
Find the maximum profit that a company can make, if the profit function is given by p(x) = 41 − 72x − 18x2.
Show that the right circular cone of least curved surface and given volume has an altitude equal to `sqrt2` time the radius of the base.
The point on the curve x2 = 2y which is nearest to the point (0, 5) is ______.
Prove that the semi-vertical angle of the right circular cone of given volume and least curved surface is \[\cot^{- 1} \left( \sqrt{2} \right)\] .
A rectangle is inscribed in a semicircle of radius r with one of its sides on the diameter of the semicircle. Find the dimensions of the rectangle to get the maximum area. Also, find the maximum area.
An open cylindrical tank whose base is a circle is to be constructed of metal sheet so as to contain a volume of `pia^3`cu cm of water. Find the dimensions so that the quantity of the metal sheet required is minimum.
Solve the following : Show that a closed right circular cylinder of given surface area has maximum volume if its height equals the diameter of its base.
Determine the maximum and minimum value of the following function.
f(x) = 2x3 – 21x2 + 36x – 20
The maximum volume of a right circular cylinder if the sum of its radius and height is 6 m is ______.
The minimum value of Z = 5x + 8y subject to x + y ≥ 5, 0 ≤ x ≤ 4, y ≥ 2, x ≥ 0, y ≥ 0 is ____________.
The maximum value of `["x"("x" − 1) + 1]^(1/3)`, 0 ≤ x ≤ 1 is:
Find all the points of local maxima and local minima of the function f(x) = (x - 1)3 (x + 1)2
Find the local minimum value of the function f(x) `= "sin"^4" x + cos"^4 "x", 0 < "x" < pi/2`
Find the points of local maxima and local minima respectively for the function f(x) = sin 2x - x, where `-pi/2 le "x" le pi/2`
Find both the maximum and minimum values respectively of 3x4 - 8x3 + 12x2 - 48x + 1 on the interval [1, 4].
The distance of that point on y = x4 + 3x2 + 2x which is nearest to the line y = 2x - 1 is ____________.
Let A = [aij] be a 3 × 3 matrix, where
aij = `{{:(1, "," if "i" = "j"),(-x, "," if |"i" - "j"| = 1),(2x + 1, "," "otherwise"):}`
Let a function f: R→R be defined as f(x) = det(A). Then the sum of maximum and minimum values of f on R is equal to ______.
Let f(x) = (x – a)ng(x) , where g(n)(a) ≠ 0; n = 0, 1, 2, 3.... then ______.
A rod AB of length 16 cm. rests between the wall AD and a smooth peg, 1 cm from the wall and makes an angle θ with the horizontal. The value of θ for which the height of G, the midpoint of the rod above the peg is minimum, is ______.
If f(x) = `1/(4x^2 + 2x + 1); x ∈ R`, then find the maximum value of f(x).
Find the maximum profit that a company can make, if the profit function is given by P(x) = 72 + 42x – x2, where x is the number of units and P is the profit in rupees.
A metal wire of 36 cm long is bent to form a rectangle. Find its dimensions when its area is maximum.
