Advertisements
Advertisements
प्रश्न
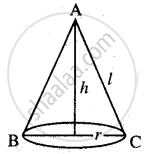
Show that the right circular cone of least curved surface and given volume has an altitude equal to `sqrt2` time the radius of the base.
Advertisements
उत्तर
Let the radius of the cone = r
Height of the cone = h
`therefore V = 1/3 pir^2 "h"` = constant quantity
`therefore r^2h = (3 xx "constant quantity")/pi = k` (assumed)
`r^2h = k, h = k/r^2` ...(1)
Curved surface S = `pirl = pir sqrt(h^2 + r^2)`
S = `pir sqrt(k^2/r^4 + r^2)`
`= pir sqrt((k^2 + r^6)/r^4)`
`= pi/r sqrt(k^2 + r^6)`
On differentiating,
`therefore (ds)/(dr) = pi [((6r^5)/(2sqrt(r^6 + k^2)) xx r - sqrt(r^6 + k^2) * 1)/r^2]`
`= pi * (3r^6 - (r^6 + k^2))/(r^2 sqrt(r^6 + k^2))`
`= (2r^6 - k^2)/(r^2 sqrt(r^6 + k^2))`
For maximum and minimum, `(dS)/(dr) = 0`
`=> 2r^6 - k^2 = 0`
`=> r^6 = k^2/2`
`=> r^6 = (h^2 r^4)/2` ...(2)
⇒ h2 = 2r2
∴ h = `sqrt2 r`
At h = `sqrt2 r`, as r passes through `sqrt2 r`
`(dS)/(dr)` changes from -ve to +ve.
∴ S is minimum when h = `sqrt2 r`
Therefore, the height of the right circular cone with the minimum curved surface is `sqrt2` times the radius.
APPEARS IN
संबंधित प्रश्न
Find the maximum and minimum value, if any, of the function given by f(x) = |x + 2| − 1.
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
`g(x) = x/2 + 2/x, x > 0`
Find the absolute maximum value and the absolute minimum value of the following function in the given interval:
f (x) = sin x + cos x , x ∈ [0, π]
Find the absolute maximum value and the absolute minimum value of the following function in the given interval:
`f(x) = 4x - 1/x x^2, x in [-2 ,9/2]`
What is the maximum value of the function sin x + cos x?
Find two numbers whose sum is 24 and whose product is as large as possible.
Find two positive numbers whose sum is 16 and the sum of whose cubes is minimum.
A square piece of tin of side 18 cm is to made into a box without a top by cutting a square from each corner and folding up the flaps to form the box. What should be the side of the square to be cut off so that the volume of the box is the maximum possible?
Show that of all the rectangles inscribed in a given fixed circle, the square has the maximum area.
Show that the right circular cylinder of given surface and maximum volume is such that is heights is equal to the diameter of the base.
The maximum value of `[x(x −1) +1]^(1/3)` , 0 ≤ x ≤ 1 is ______.
An open tank with a square base and vertical sides is to be constructed from a metal sheet so as to hold a given quantity of water. Show that the cost of material will be least when the depth of the tank is half of its width. If the cost is to be borne by nearby settled lower-income families, for whom water will be provided, what kind of value is hidden in this question?
A given quantity of metal is to be cast into a half cylinder with a rectangular base and semicircular ends. Show that in order that the total surface area may be minimum the ratio of the length of the cylinder to the diameter of its semi-circular ends is \[\pi : (\pi + 2)\].
Find the maximum and minimum of the following functions : f(x) = x3 – 9x2 + 24x
Find the maximum and minimum of the following functions : f(x) = `x^2 + (16)/x^2`
Divide the number 20 into two parts such that sum of their squares is minimum.
Find the largest size of a rectangle that can be inscribed in a semicircle of radius 1 unit, so that two vertices lie on the diameter.
Choose the correct option from the given alternatives :
If f(x) = `(x^2 - 1)/(x^2 + 1)`, for every real x, then the minimum value of f is ______.
If f(x) = x.log.x then its maximum value is ______.
The function f(x) = x log x is minimum at x = ______.
The minimum value of Z = 5x + 8y subject to x + y ≥ 5, 0 ≤ x ≤ 4, y ≥ 2, x ≥ 0, y ≥ 0 is ____________.
If f(x) = `x + 1/x, x ne 0`, then local maximum and x minimum values of function f are respectively.
An open box with square base is to be made of a given quantity of cardboard of area c2. Show that the maximum volume of the box is `"c"^3/(6sqrt(3))` cubic units
The function f(x) = 2x3 – 3x2 – 12x + 4, has ______.
The maximum value of `(1/x)^x` is ______.
Find both the maximum and minimum values respectively of 3x4 - 8x3 + 12x2 - 48x + 1 on the interval [1, 4].
The function f(x) = x5 - 5x4 + 5x3 - 1 has ____________.
The function `f(x) = x^3 - 6x^2 + 9x + 25` has
The point on the curve `x^2 = 2y` which is nearest to the point (0, 5) is
If S1 and S2 are respectively the sets of local minimum and local maximum points of the function. f(x) = 9x4 + 12x3 – 36x2 + 25, x ∈ R, then ______.
The function g(x) = `(f(x))/x`, x ≠ 0 has an extreme value when ______.
The set of values of p for which the points of extremum of the function f(x) = x3 – 3px2 + 3(p2 – 1)x + 1 lie in the interval (–2, 4), is ______.
Find two numbers whose sum is 15 and when the square of one number multiplied by the cube of the other is maximum.
The rectangle has area of 50 cm2. Complete the following activity to find its dimensions for least perimeter.
Solution: Let x cm and y cm be the length and breadth of a rectangle.
Then its area is xy = 50
∴ `y =50/x`
Perimeter of rectangle `=2(x+y)=2(x+50/x)`
Let f(x) `=2(x+50/x)`
Then f'(x) = `square` and f''(x) = `square`
Now,f'(x) = 0, if x = `square`
But x is not negative.
∴ `x = root(5)(2) "and" f^('')(root(5)(2))=square>0`
∴ by the second derivative test f is minimum at x = `root(5)(2)`
When x = `root(5)(2),y=50/root(5)(2)=root(5)(2)`
∴ `x=root(5)(2) "cm" , y = root(5)(2) "cm"`
Hence, rectangle is a square of side `root(5)(2) "cm"`
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
f(x) `= x sqrt(1 - x), 0 < x < 1`
If \[\mathrm{A}+\mathrm{B}=\frac{\pi}{2}\] then the maximum value of cosA.cosB is
What are the critical points obtained from \[12x(x-1)(x+2)=0\]?
