Advertisements
Advertisements
प्रश्न
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
`g(x) = 1/(x^2 + 2)`
उत्तर
Given, `g (x) = 1/ (x^2 + 2)`
= `g' (x) = (-2x)/(x^2 + 2)^2`
For critical points, let g' (x) = 0
= `(-2x)/(x^2 + 2)^2 = 0`
x = 0 ....(∵ x2 + 2 ≠ 0)
`g'' (x) = (6x^2 - 4)/(x^2 + 2)^3; g'' (0) = (-4)/8 <0`
∴ g has a local maximum at x = 0 and local
maximum value is `g (0) = 1/ (0 + 2) = 1/2`
APPEARS IN
संबंधित प्रश्न
Find the maximum and minimum value, if any, of the following function given by g(x) = − |x + 1| + 3.
Find the maximum and minimum value, if any, of the following function given by f(x) = |sin 4x + 3|
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
`h(x) = sinx + cosx, 0 < x < pi/2`
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
f(x) = x3 − 6x2 + 9x + 15
Find the local maxima and local minima, if any, of the following functions. Find also the local maximum and the local minimum values, as the case may be:
`f(x) = xsqrt(1-x), x > 0`
Prove that the following function do not have maxima or minima:
g(x) = logx
Find the absolute maximum value and the absolute minimum value of the following function in the given interval:
`f(x) = 4x - 1/x x^2, x in [-2 ,9/2]`
What is the maximum value of the function sin x + cos x?
Of all the closed cylindrical cans (right circular), of a given volume of 100 cubic centimetres, find the dimensions of the can which has the minimum surface area?
Find the absolute maximum and minimum values of the function f given by f (x) = cos2 x + sin x, x ∈ [0, π].
A rod of 108 meters long is bent to form a rectangle. Find its dimensions if the area is maximum. Let x be the length and y be the breadth of the rectangle.
Find the largest size of a rectangle that can be inscribed in a semicircle of radius 1 unit, so that two vertices lie on the diameter.
Show that the height of a closed right circular cylinder of given volume and least surface area is equal to its diameter.
Find the volume of the largest cylinder that can be inscribed in a sphere of radius ‘r’ cm.
Solve the following : Show that of all rectangles inscribed in a given circle, the square has the maximum area.
Solve the following : Show that a closed right circular cylinder of given surface area has maximum volume if its height equals the diameter of its base.
Solve the following : Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is `(4r)/(3)`.
Examine the function for maxima and minima f(x) = x3 - 9x2 + 24x
A wire of length 120 cm is bent in the form of a rectangle. Find its dimensions if the area of the rectangle is maximum
The maximum value of function x3 - 15x2 + 72x + 19 in the interval [1, 10] is ______.
The two parts of 120 for which the sum of double of first and square of second part is minimum, are ______.
The sum of two non-zero numbers is 6. The minimum value of the sum of their reciprocals is ______.
Find all the points of local maxima and local minima of the function f(x) = `- 3/4 x^4 - 8x^3 - 45/2 x^2 + 105`
If the sum of the lengths of the hypotenuse and a side of a right-angled triangle is given, show that the area of the triangle is maximum when the angle between them is `pi/3`
The sum of the surface areas of a rectangular parallelopiped with sides x, 2x and `x/3` and a sphere is given to be constant. Prove that the sum of their volumes is minimum, if x is equal to three times the radius of the sphere. Also find the minimum value of the sum of their volumes.
The function f(x) = 2x3 – 3x2 – 12x + 4, has ______.
The curves y = 4x2 + 2x – 8 and y = x3 – x + 13 touch each other at the point ______.
Find the maximum profit that a company can make, if the profit function is given by P(x) = 41 + 24x – 18x2.
Find both the maximum and minimum values respectively of 3x4 - 8x3 + 12x2 - 48x + 1 on the interval [1, 4].
The distance of that point on y = x4 + 3x2 + 2x which is nearest to the line y = 2x - 1 is ____________.
The range of a ∈ R for which the function f(x) = `(4a - 3)(x + log_e5) + 2(a - 7)cot(x/2)sin^2(x/2), x ≠ 2nπ, n∈N` has critical points, is ______.
Let P(h, k) be a point on the curve y = x2 + 7x + 2, nearest to the line, y = 3x – 3. Then the equation of the normal to the curve at P is ______.
The minimum value of 2sinx + 2cosx is ______.
The maximum value of z = 6x + 8y subject to constraints 2x + y ≤ 30, x + 2y ≤ 24 and x ≥ 0, y ≥ 0 is ______.
A straight line is drawn through the point P(3, 4) meeting the positive direction of coordinate axes at the points A and B. If O is the origin, then minimum area of ΔOAB is equal to ______.
Divide the number 100 into two parts so that the sum of their squares is minimum.
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
f(x) `= x sqrt(1 - x), 0 < x < 1`
Sumit has bought a closed cylindrical dustbin. The radius of the dustbin is ‘r' cm and height is 'h’ cm. It has a volume of 20π cm3.
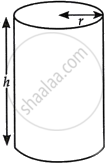
- Express ‘h’ in terms of ‘r’, using the given volume.
- Prove that the total surface area of the dustbin is `2πr^2 + (40π)/r`
- Sumit wants to paint the dustbin. The cost of painting the base and top of the dustbin is ₹ 2 per cm2 and the cost of painting the curved side is ₹ 25 per cm2. Find the total cost in terms of ‘r’, for painting the outer surface of the dustbin including the base and top.
- Calculate the minimum cost for painting the dustbin.
