Advertisements
Advertisements
प्रश्न
Examine the function for maxima and minima f(x) = x3 - 9x2 + 24x
उत्तर
f(x) = x3 - 9x2 + 24x
∴ f '(x) = 3x2 - 18x + 24
∴ f ''(x) = 6x - 18
Consider, f '(x) = 0
∴ 3x2 - 18x + 24 = 0
∴ 3(x2 - 6x + 8) = 0
∴ 3(x - 4)(x - 2) = 0
∴ (x - 4)(x - 2) = 0
∴ x = 2 or x = 4
For x = 4,
f ''(4) = 6(4) - 18 = 24 - 18 = 6 > 0
∴ f(x) is minimum at x = 4
∴ Minima = f(4) = (4)3 - 9(4)2 + 24(4)
= 64 - 144 + 96 = 16
For x = 2,
f ''(2) = 6(2) - 18 = 12 - 18 = - 6 < 0
∴ f(x) is maximum at x = 2
∴ Maxima = f(2) = (2)3 - 9(2)2 + 24(2) = 8 - 36 + 48 = 20
∴ Maxima = 20 and Minima = 16
APPEARS IN
संबंधित प्रश्न
Find the maximum and minimum value, if any, of the following function given by f(x) = −(x − 1)2 + 10
Find the absolute maximum value and the absolute minimum value of the following function in the given interval:
f (x) = sin x + cos x , x ∈ [0, π]
Find the absolute maximum value and the absolute minimum value of the following function in the given interval:
`f(x) = 4x - 1/x x^2, x in [-2 ,9/2]`
Find both the maximum value and the minimum value of 3x4 − 8x3 + 12x2 − 48x + 25 on the interval [0, 3].
Prove that the volume of the largest cone that can be inscribed in a sphere of radius R is `8/27` of the volume of the sphere.
A window is in the form of a rectangle surmounted by a semicircular opening. The total perimeter of the window is 10 m. Find the dimensions of the window to admit maximum light through the whole opening
A point on the hypotenuse of a triangle is at distance a and b from the sides of the triangle.
Show that the minimum length of the hypotenuse is `(a^(2/3) + b^(2/3))^(3/2).`
The volume of a closed rectangular metal box with a square base is 4096 cm3. The cost of polishing the outer surface of the box is Rs. 4 per cm2. Find the dimensions of the box for the minimum cost of polishing it.
The profit function P(x) of a firm, selling x items per day is given by P(x) = (150 – x)x – 1625 . Find the number of items the firm should manufacture to get maximum profit. Find the maximum profit.
Solve the following : An open box with a square base is to be made out of given quantity of sheet of area a2. Show that the maximum volume of the box is `a^3/(6sqrt(3)`.
If R is the circum radius of Δ ABC, then A(Δ ABC) = ______.
AB is a diameter of a circle and C is any point on the circle. Show that the area of ∆ABC is maximum, when it is isosceles.
The maximum value of `(1/x)^x` is ______.
The maximum value of `[x(x - 1) + 1]^(2/3), 0 ≤ x ≤ 1` is
Let f(x) = (x – a)ng(x) , where g(n)(a) ≠ 0; n = 0, 1, 2, 3.... then ______.
Complete the following activity to divide 84 into two parts such that the product of one part and square of the other is maximum.
Solution: Let one part be x. Then the other part is 84 - x
Letf (x) = x2 (84 - x) = 84x2 - x3
∴ f'(x) = `square`
and f''(x) = `square`
For extreme values, f'(x) = 0
∴ x = `square "or" square`
f(x) attains maximum at x = `square`
Hence, the two parts of 84 are 56 and 28.
Find the point on the curve y2 = 4x, which is nearest to the point (2, 1).
Determine the minimum value of the function.
f(x) = 2x3 – 21x2 + 36x – 20
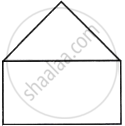
Mrs. Roy designs a window in her son’s study room so that the room gets maximum sunlight. She designs the window in the shape of a rectangle surmounted by an equilateral triangle. If the perimeter of the window is 12 m, find the dimensions of the window that will admit maximum sunlight into the room.
Sumit has bought a closed cylindrical dustbin. The radius of the dustbin is ‘r' cm and height is 'h’ cm. It has a volume of 20π cm3.
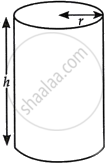
- Express ‘h’ in terms of ‘r’, using the given volume.
- Prove that the total surface area of the dustbin is `2πr^2 + (40π)/r`
- Sumit wants to paint the dustbin. The cost of painting the base and top of the dustbin is ₹ 2 per cm2 and the cost of painting the curved side is ₹ 25 per cm2. Find the total cost in terms of ‘r’, for painting the outer surface of the dustbin including the base and top.
- Calculate the minimum cost for painting the dustbin.
