Question

Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is `(4r)/3`. Also find maximum volume in terms of volume of the sphere

Show that the altitude of a right circular cone of maximum volume that can be inscribed in a sphere of radius r is `(4r)/3` . Also, show that the maximum volume of the cone is `8/27`  of the volume of the sphere.

Answer 1

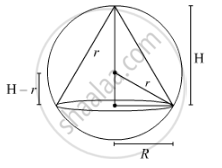
`V=1/3piR^2H`
It is clear from the figure that

`R^2+(H−r)^2=r^2`

`⇒R^2+H^2+r^2−2Hr=r^2`

`⇒R^2=2Hr−H^2`

Substituting the value of R² in the formula for the volume of the cone, we get

`V=1/3pi(2Hr-H^2)H`

` V=2/3πrH^2−π/3H^3`

 

Differentiating with respect to H both sides, we get:

`(dV)/(dH)=4/3πrH−πH^2`

At critical point,`(dV)/(dH)` is 0.

`⇒4/3πrH−πH^2=0`

`⇒H=4/3r`

Differentiating V w.r.t H again, we get:

`(d^2V)/(dH^2)=4/3πr−2πH`

`|(d^2V)/(dH^2)|_(H=4/3r)=−4/3πr <0`

Hence maxima.

Volume of cone =`1/3πR^2H`

` V=2/3πrH^2−π/3H^3`

Substituting the value of H, we get:

`V=2/3πr(4/3r)^2−π/3(4/3r)^3`

`=>V=8/27(4πr^3−8/3πr^3)`

`=>V=8/27(4/3πr^3)`

`=>V=8/27(volume of sphere)`

 

Answer 2

A sphere of fixed radius (r) is given.

Let R and h be the radius and the height of the cone, respectively.

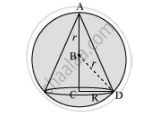
The volume (V) of the cone is given by,

`V=1/3piR^2h`

Now, from the right triangle BCD, we have:

`BC=sqrt(r^2-R^2)`

`:.h=r+sqrt(r^2-R^2)`

 `V=1/3piR^2(r+sqrt(r^2-R^2))=1/3piR^2r+1/3piR^2sqrt(r^2-R^2)`

`(dV)/(dR)=2/3piRr+2/3piRsqrt(r^2-R^2)+(piR^2)/3 (-2R)/(2sqrt(r^2-R^2))`

`=2/3piRr+2/3piRsqrt(r^2-R^2)-(piR^3)/(3sqrt(r^2-R^2))`

`=2/3piRr+(2piR(r^2-R^2)-piR^3)/(3sqrt(r^2-R^2))`

`2/3piRr+(2piRr^2-3piR^3)/(3sqrt(r^2-R^2))`

Now  

`(dV)/(dR^2)=0`

`=>(2pirR)/3=(3piR^3-2piRr^2)/(3sqrt(r^2-R^2))`

`=>2rsqrt(r^2-R^2)=3R^2-2r^2`

`=>4r^2(r^2-R^2)=(3R^2-2r^2)^2`

`=>4r^4-4r^2R^2=9R^4+4r^4-12R^2r^2`

`=>9R^4-8r^2R^2=0`

`=>9R^2=8r^2`

`=>R^2=(8r^2)/9`

Now,

`(d^2V)/(dR^2)=(2pir)/3+(3sqrt(r^2-R^2)(2pir^2-9piR^2)-(2piRr^2-3piR^3)(-6R)1/(2sqrtr^2-R^2))/(9(r^2-R^2))`

 

`=(2pir)/3+(3sqrt(r^2-R^2) (2pir^2-9piR^2)+(2piRr^2-3piR^3)(3R)1/(2sqrt(r^2-R^2)))/(9(r^2-R^2))`

 

Now when `R^2=(8r^2)/9`it can be shown that `(d^2V)/(dR^2)<0`

∴ The volume is the maximum when `R^2=(8r^2)/9`

When `R^2=(8r^2)/9`height of cone= `r+sqrt(r^2-(8r^2)/9)=r+sqrt(r^2/9)=r+r/3=(4r)/3`

Hence, it can be seen that the altitude of a right circular cone of maximum volume that can be inscribed in a sphere of radius r is `(4r)/3`

Let volume of the sphere be `V_s=4/3pir^3`

`r=3sqrt((3V_s)/(4pi))`

∴ Volume of cone, V = `1/3piR^2h`

⇒R = `(2sqrt2)/3r`

V = `1/3pi((2sqrt2)/3r)xx(4r)/3`

⇒V = `1/3pi(8r^2)/9xx(4r)/3`

`V=(32pir^3)/81=32/81pi[(3V_s)/(4pi)]`

∴ Volume of cone in terms of sphere