Advertisements
Advertisements
प्रश्न
An open tank with a square base and vertical sides is to be constructed from a metal sheet so as to hold a given quantity of water. Show that the cost of material will be least when the depth of the tank is half of its width. If the cost is to be borne by nearby settled lower-income families, for whom water will be provided, what kind of value is hidden in this question?
उत्तर
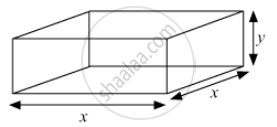
The base of the tank is square.
Let the length, width and height of the open tank be x, x and y units respectively.
Volume = Length × Breadth × Height = x2 y
Total surface area = 2(lb + bh + hl) − lb = x2 + 4xy.
The volume of the tank is given to be constant
Now, surface area = x2 + 4xy
For the total surface area to be least
Hence, the surface area is minimum when x = 2y, i.e., the depth of the tank is half of its width.
Now if the surface area of the sheet is minimum the cost of the sheet will be least as well, Thus making the tank economical and cost-effective.
APPEARS IN
संबंधित प्रश्न
Find the approximate value of cos (89°, 30'). [Given is: 1° = 0.0175°C]
Find the maximum and minimum value, if any, of the following function given by h(x) = sin(2x) + 5.
Find the local maxima and local minima, if any, of the following function. Find also the local maximum and the local minimum values, as the case may be:
`h(x) = sinx + cosx, 0 < x < pi/2`
Prove that the following function do not have maxima or minima:
g(x) = logx
Find both the maximum value and the minimum value of 3x4 − 8x3 + 12x2 − 48x + 25 on the interval [0, 3].
At what points in the interval [0, 2π], does the function sin 2x attain its maximum value?
Find two numbers whose sum is 24 and whose product is as large as possible.
Find two positive numbers x and y such that x + y = 60 and xy3 is maximum.
Find two positive numbers x and y such that their sum is 35 and the product x2y5 is a maximum.
Find the maximum and minimum of the following functions : f(x) = `logx/x`
Divide the number 20 into two parts such that sum of their squares is minimum.
Solve the following:
A rectangular sheet of paper of fixed perimeter with the sides having their lengths in the ratio 8 : 15 converted into an open rectangular box by folding after removing the squares of equal area from all corners. If the total area of the removed squares is 100, the resulting box has maximum volume. Find the lengths of the rectangular sheet of paper.
Solve the following : Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is `(2"R")/sqrt(3)`. Also, find the maximum volume.
Find all the points of local maxima and local minima of the function f(x) = `- 3/4 x^4 - 8x^3 - 45/2 x^2 + 105`
Find the points of local maxima, local minima and the points of inflection of the function f(x) = x5 – 5x4 + 5x3 – 1. Also find the corresponding local maximum and local minimum values.
An open box with square base is to be made of a given quantity of cardboard of area c2. Show that the maximum volume of the box is `"c"^3/(6sqrt(3))` cubic units
Find the points of local maxima and local minima respectively for the function f(x) = sin 2x - x, where `-pi/2 le "x" le pi/2`
The area of a right-angled triangle of the given hypotenuse is maximum when the triangle is ____________.
Find the area of the largest isosceles triangle having a perimeter of 18 meters.
Let f(x) = 1 + 2x2 + 22x4 + …… + 210x20. Then f (x) has ____________.
For all real values of `x`, the minimum value of `(1 - x + x^2)/(1 + x + x^2)`
Divide 20 into two ports, so that their product is maximum.
A wire of length 36 m is cut into two pieces, one of the pieces is bent to form a square and the other is bent to form a circle. If the sum of the areas of the two figures is minimum, and the circumference of the circle is k (meter), then `(4/π + 1)`k is equal to ______.
Let f(x) = (x – a)ng(x) , where g(n)(a) ≠ 0; n = 0, 1, 2, 3.... then ______.
The sum of all the local minimum values of the twice differentiable function f : R `rightarrow` R defined by
f(x) = `x^3 - 3x^2 - (3f^('')(2))/2 x + f^('')(1)`
If Mr. Rane order x chairs at the price p = (2x2 - 12x - 192) per chair. How many chairs should he order so that the cost of deal is minimum?
Solution: Let Mr. Rane order x chairs.
Then the total price of x chairs = p·x = (2x2 - 12x- 192)x
= 2x3 - 12x2 - 192x
Let f(x) = 2x3 - 12x2 - 192x
∴ f'(x) = `square` and f''(x) = `square`
f'(x ) = 0 gives x = `square` and f''(8) = `square` > 0
∴ f is minimum when x = 8
Hence, Mr. Rane should order 8 chairs for minimum cost of deal.
The rectangle has area of 50 cm2. Complete the following activity to find its dimensions for least perimeter.
Solution: Let x cm and y cm be the length and breadth of a rectangle.
Then its area is xy = 50
∴ `y =50/x`
Perimeter of rectangle `=2(x+y)=2(x+50/x)`
Let f(x) `=2(x+50/x)`
Then f'(x) = `square` and f''(x) = `square`
Now,f'(x) = 0, if x = `square`
But x is not negative.
∴ `x = root(5)(2) "and" f^('')(root(5)(2))=square>0`
∴ by the second derivative test f is minimum at x = `root(5)(2)`
When x = `root(5)(2),y=50/root(5)(2)=root(5)(2)`
∴ `x=root(5)(2) "cm" , y = root(5)(2) "cm"`
Hence, rectangle is a square of side `root(5)(2) "cm"`
Find the maximum and the minimum values of the function f(x) = x2ex.
Find the point on the curve y2 = 4x, which is nearest to the point (2, 1).
Sumit has bought a closed cylindrical dustbin. The radius of the dustbin is ‘r' cm and height is 'h’ cm. It has a volume of 20π cm3.
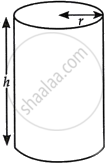
- Express ‘h’ in terms of ‘r’, using the given volume.
- Prove that the total surface area of the dustbin is `2πr^2 + (40π)/r`
- Sumit wants to paint the dustbin. The cost of painting the base and top of the dustbin is ₹ 2 per cm2 and the cost of painting the curved side is ₹ 25 per cm2. Find the total cost in terms of ‘r’, for painting the outer surface of the dustbin including the base and top.
- Calculate the minimum cost for painting the dustbin.
