Advertisements
Advertisements
Question
An open tank with a square base and vertical sides is to be constructed from a metal sheet so as to hold a given quantity of water. Show that the cost of material will be least when the depth of the tank is half of its width. If the cost is to be borne by nearby settled lower-income families, for whom water will be provided, what kind of value is hidden in this question?
Solution
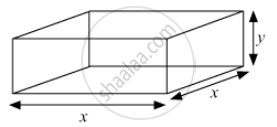
The base of the tank is square.
Let the length, width and height of the open tank be x, x and y units respectively.
Volume = Length × Breadth × Height = x2 y
Total surface area = 2(lb + bh + hl) − lb = x2 + 4xy.
The volume of the tank is given to be constant
Now, surface area = x2 + 4xy
For the total surface area to be least
Hence, the surface area is minimum when x = 2y, i.e., the depth of the tank is half of its width.
Now if the surface area of the sheet is minimum the cost of the sheet will be least as well, Thus making the tank economical and cost-effective.
APPEARS IN
RELATED QUESTIONS
Examine the maxima and minima of the function f(x) = 2x3 - 21x2 + 36x - 20 . Also, find the maximum and minimum values of f(x).
Find the approximate value of cos (89°, 30'). [Given is: 1° = 0.0175°C]
Find the maximum and minimum value, if any, of the following function given by f(x) = |sin 4x + 3|
Find the local maxima and local minima, if any, of the following functions. Find also the local maximum and the local minimum values, as the case may be:
`f(x) = xsqrt(1-x), x > 0`
What is the maximum value of the function sin x + cos x?
Find the maximum and minimum values of x + sin 2x on [0, 2π].
Find two positive numbers whose sum is 16 and the sum of whose cubes is minimum.
A square piece of tin of side 18 cm is to made into a box without a top by cutting a square from each corner and folding up the flaps to form the box. What should be the side of the square to be cut off so that the volume of the box is the maximum possible?
The maximum value of `[x(x −1) +1]^(1/3)` , 0 ≤ x ≤ 1 is ______.
A point on the hypotenuse of a triangle is at distance a and b from the sides of the triangle.
Show that the minimum length of the hypotenuse is `(a^(2/3) + b^(2/3))^(3/2).`
Show that the surface area of a closed cuboid with square base and given volume is minimum, when it is a cube.
A metal box with a square base and vertical sides is to contain 1024 cm3. The material for the top and bottom costs Rs 5 per cm2 and the material for the sides costs Rs 2.50 per cm2. Find the least cost of the box
Find the maximum and minimum of the following functions : f(x) = `logx/x`
Divide the number 20 into two parts such that sum of their squares is minimum.
Choose the correct option from the given alternatives :
If f(x) = `(x^2 - 1)/(x^2 + 1)`, for every real x, then the minimum value of f is ______.
The minimum value of Z = 5x + 8y subject to x + y ≥ 5, 0 ≤ x ≤ 4, y ≥ 2, x ≥ 0, y ≥ 0 is ____________.
Twenty meters of wire is available for fencing off a flowerbed in the form of a circular sector. Then the maximum area (in sq. m) of the flower-bed, is ______
The minimum value of the function f(x) = 13 - 14x + 9x2 is ______
Find all the points of local maxima and local minima of the function f(x) = `- 3/4 x^4 - 8x^3 - 45/2 x^2 + 105`
Find all the points of local maxima and local minima of the function f(x) = (x - 1)3 (x + 1)2
If y `= "ax - b"/(("x" - 1)("x" - 4))` has a turning point P(2, -1), then find the value of a and b respectively.
Find the height of the cylinder of maximum volume that can be inscribed in a sphere of radius a.
The range of a ∈ R for which the function f(x) = `(4a - 3)(x + log_e5) + 2(a - 7)cot(x/2)sin^2(x/2), x ≠ 2nπ, n∈N` has critical points, is ______.
The minimum value of 2sinx + 2cosx is ______.
The maximum value of f(x) = `logx/x (x ≠ 0, x ≠ 1)` is ______.
Find two numbers whose sum is 15 and when the square of one number multiplied by the cube of the other is maximum.
Find the point on the curve y2 = 4x, which is nearest to the point (2, 1).
