Advertisements
Advertisements
प्रश्न
If the sum of the surface areas of cube and a sphere is constant, what is the ratio of an edge of the cube to the diameter of the sphere, when the sum of their volumes is minimum?
उत्तर
Let x be the edge of the cube and r be the radius of the sphere.
Surface area of cube = 6x2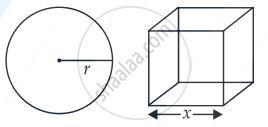
And surface area of the sphere = 4πr2
∴ 6x2 + 4πr2 = K ......(constant)
⇒ r = `sqrt(("K" - 6x^2)/(4pi)` .....(i)
Volume of the cube = x3 and the volume of sphere = `3/4 pi"r"^3`
∴ Sum of their volumes (V) = Volume of cube + Volume of sphere
⇒ V = `x^3 + 4/3 pi"r"^3`
⇒ V = `x^3 + 4/3 pi xx (("K" - 6x^2)/(4pi))^(3/2)`
Differentiating both sides w.r.t. x, we get
`"dV"/"dx" = 3x^2 + (4pi)/3 xx 3/2("K" - 6x^2)^(1/2) (- 12x) xx 1/((4pi)^(3/2)`
= `3x^2 + (2pi)/((4pi)^(3/2)) xx (-12x) ("K" - 6x^2)^(1/2)`
= `3x^2 + 1/(4pi^(1/2)) xx (-12x) ("K" - 6x^2)^(1/2)`
∴ `"dV"/"dx" = 3x^2 - (3x)/sqrt(pi) ("K" - 6x^2)^(1/2)` ....(ii)
For local maxima and local minima, `"dV"/"dx"` = 0
∴ `3x^2 - (3x)/sqrt(pi) ("K" - 6x^2)^(1/2)` = 0
⇒ `3x[x - ("k" - 6x^2)^(1/2)/sqrt(pi)]` = 0
x ≠ 0
∴ `x - ("K" - 6x^2)^(1/2)/sqrt(pi)` = 0
⇒ x = `("K" - 6x^2)^(1/2)/sqrt(pi)`
Squaring both sides, we get
x2 = `("K" - 6x^2)/pi`
⇒ `pix^2 = "K" - 6x^2`
⇒ `pix^2 + 6x^2` = K
⇒ `x^2(pi + 6)` = K
⇒ x2 = `"K"/(pi + 6)`
∴ x = `sqrt("K"/(pi + 6)`
Now putting the value of K in equation (i), we get
`6x^2 + 4pir^2 = x^2(pi + 6)`
⇒ `6x^2 + 4pi"r"^2 = pix^2 + 6x^2`
⇒ `4pi"r"^2 = pi"r"^2`
⇒ 4r2 = x2
∴ 2r = x
∴ x:2r = 1:1
Now differentiating equation (ii) w.r.t x, we have
`("d"^2"V")/("dx"^2) = 6x - 3/sqrt(pi) "d"/"dx" [x("K" - 6x^2)^(1/2)]`
= `6x - 3/sqrt(pi)[x * 1/(2sqrt("K" - 6x^2)) xx (-12x) + ("K" - 6x^2)^(1/2) * 1]`
= `6x - 3/sqrt(pi) [(-6x^2)/sqrt("K" - 6x^2) + sqrt("K" - 6x^2)]`
= `6x - 3/sqrt(pi) [(-6x^2 + "K" - 6x^2)/sqrt("K" - 6x^2)]`
= `6x + 3/sqrt(pi) [(12x^2 - "K")/sqrt("K" - 6x^2)]`
Put x = `sqrt("K"/(pi + 6)`
= `6sqrt("K"/(pi + 6)) + 3/sqrt(pi)[((12"K")/(pi + 6) - "K")/sqrt("K" - (6"K")/(pi + 6))]`
= `6sqrt("K"/(pi + 6)) + 3/sqrt(pi) [(12"K" - pi"K" - 6"K")/sqrt((pi"K" + 6"K" - 6"K")/(pi + 6))]`
= `6sqrt("K"/(pi + 6)) + 3/sqrt(pi) [(6"K" - pi"K")/sqrt((pi"K")/(pi + 6))]`
= `6sqrt("K"/(pi + 6)) + 3/(pisqrt("K"))[(6"K" - pi"K") sqrt(pi + 6)] > 0`
So it is minima.
Hence, the required ratio is 1 : 1 when the combined volume is minimum.
APPEARS IN
संबंधित प्रश्न
Find the maximum and minimum value, if any, of the following function given by f(x) = −(x − 1)2 + 10
Find the maximum and minimum value, if any, of the function given by f(x) = |x + 2| − 1.
Find the maximum and minimum value, if any, of the following function given by f(x) = |sin 4x + 3|
Prove that the following function do not have maxima or minima:
h(x) = x3 + x2 + x + 1
Find the absolute maximum value and the absolute minimum value of the following function in the given interval:
`f(x) = 4x - 1/x x^2, x in [-2 ,9/2]`
At what points in the interval [0, 2π], does the function sin 2x attain its maximum value?
Find two positive numbers x and y such that x + y = 60 and xy3 is maximum.
Find the absolute maximum and minimum values of the function f given by f (x) = cos2 x + sin x, x ∈ [0, π].
Show that the surface area of a closed cuboid with square base and given volume is minimum, when it is a cube.
An open tank with a square base and vertical sides is to be constructed from a metal sheet so as to hold a given quantity of water. Show that the cost of material will be least when the depth of the tank is half of its width. If the cost is to be borne by nearby settled lower-income families, for whom water will be provided, what kind of value is hidden in this question?
A wire of length 36 metres is bent in the form of a rectangle. Find its dimensions if the area of the rectangle is maximum.
A metal wire of 36cm long is bent to form a rectangle. Find it's dimensions when it's area is maximum.
Find the local maximum and local minimum value of f(x) = x3 − 3x2 − 24x + 5
A rectangular sheet of paper has it area 24 sq. Meters. The margin at the top and the bottom are 75 cm each and the sides 50 cm each. What are the dimensions of the paper if the area of the printed space is maximum?
Divide the number 20 into two parts such that their product is maximum
A rod of 108 m long is bent to form a rectangle. Find it’s dimensions when it’s area is maximum.
Twenty meters of wire is available for fencing off a flowerbed in the form of a circular sector. Then the maximum area (in sq. m) of the flower-bed, is ______
The function y = 1 + sin x is maximum, when x = ______
The maximum value of function x3 - 15x2 + 72x + 19 in the interval [1, 10] is ______.
Show that the function f(x) = 4x3 – 18x2 + 27x – 7 has neither maxima nor minima.
The sum of the surface areas of a rectangular parallelopiped with sides x, 2x and `x/3` and a sphere is given to be constant. Prove that the sum of their volumes is minimum, if x is equal to three times the radius of the sphere. Also find the minimum value of the sum of their volumes.
The smallest value of the polynomial x3 – 18x2 + 96x in [0, 9] is ______.
Find both the maximum and minimum values respectively of 3x4 - 8x3 + 12x2 - 48x + 1 on the interval [1, 4].
The function g(x) = `(f(x))/x`, x ≠ 0 has an extreme value when ______.
The set of values of p for which the points of extremum of the function f(x) = x3 – 3px2 + 3(p2 – 1)x + 1 lie in the interval (–2, 4), is ______.
The greatest value of the function f(x) = `tan^-1x - 1/2logx` in `[1/sqrt(3), sqrt(3)]` is ______.
The minimum value of the function f(x) = xlogx is ______.
A right circular cylinder is to be made so that the sum of the radius and height is 6 metres. Find the maximum volume of the cylinder.
Determine the minimum value of the function.
f(x) = 2x3 – 21x2 + 36x – 20
