Advertisements
Advertisements
Question
Use product `[(1,-1,2),(0,2,-3),(3,-2,4)][(-2,0,1),(9,2,-3),(6,1,-2)]` to solve the system of equations x + 3z = 9, −x + 2y − 2z = 4, 2x − 3y + 4z = −3
Solution

Since, A × B = I,
∴ B = A−1 .....(1)
Now, the given system of equations is
x + 3z = 9
−x + 2y − 2z = 4
2x − 3y + 4z = −3
This can also be represented as,

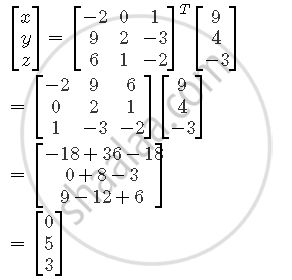
Hence, x = 0, y = 5 and z = 3.
APPEARS IN
RELATED QUESTIONS
Find the value of x, y, and z from the following equation:
`[(x+y+z), (x+z), (y+z)] = [(9),(5),(7)]`
if `A = [(0, -tan alpha/2), (tan alpha/2, 0)]` and I is the identity matrix of order 2, show that I + A = `(I -A)[(cos alpha, -sin alpha),(sin alpha, cos alpha)]`
Let A = `[(0,1),(0,0)]`show that (aI+bA)n = anI + nan-1 bA , where I is the identity matrix of order 2 and n ∈ N
A coaching institute of English (subject) conducts classes in two batches I and II and fees for rich and poor children are different. In batch I, it has 20 poor and 5 rich children and total monthly collection is Rs 9,000, whereas in batch II, it has 5 poor and 25 rich children and total monthly collection is Rs 26,000. Using matrix method, find monthly fees paid by each child of two types. What values the coaching institute is inculcating in the society?
If 𝒙 = r cos θ and y= r sin θ prove that JJ-1=1.
If\[A = \begin{bmatrix}2 & 3 \\ 4 & 5\end{bmatrix}\]prove that A − AT is a skew-symmetric matrix.
Classify the following matrix as, a row, a column, a square, a diagonal, a scalar, a unit, an upper triangular, a lower triangular, a symmetric or a skew-symmetric matrix:
`[(2, 0, 0),(3, -1, 0),(-7, 3, 1)]`
Identify the following matrix is singular or non-singular?
`[("a", "b", "c"),("p", "q", "r"),(2"a" - "p", 2"b" - "q", 2"c" - "r")]`
Identify the following matrix is singular or non-singular?
`[(5, 0, 5),(1, 99, 100),(6, 99, 105)]`
Identify the following matrix is singular or non-singular?
`[(3, 5, 7),(-2, 1, 4),(3, 2, 5)]`
Find k if the following matrix is singular:
`[(7, 3),(-2, "k")]`
If A = `[(5, 1, -1),(3, 2, 0)]`, Find (AT)T.
Find x, y, z If `[(0, -5"i", x),(y, 0, z),(3/2, -sqrt(2), 0)]` is a skew symmetric matrix.
The following matrix, using its transpose state whether it is symmetric, skew-symmetric, or neither:
`[(0, 1 + 2"i", "i" - 2),(-1 - 2"i", 0, -7),(2 - "i", 7, 0)]`
Construct the matrix A = [aij]3 × 3 where aij = i − j. State whether A is symmetric or skew-symmetric.
Answer the following question:
If A = diag [2 –3 –5], B = diag [4 –6 –3] and C = diag [–3 4 1] then find 2A + B – 5C
Answer the following question:
If A = `[(1, 2, 3),(2, 4, 6),(1, 2, 3)]`, B = `[(1, -1, 1),(-3, 2, -1),(-2, 1, 0)]`, show that AB and BA are both singular matrices
If A = `[(6, 0),("p", "q")]` is a scalar matrix, then the values of p and q are ______ respectively.
If A and B are matrices of same order, then (3A –2B)′ is equal to______.
A square matrix B = [bÿ] m × m is said to be a diagonal matrix if all diagonal elements are
If all the elements are zero, then matrix is said to be
A = `[a_(ij)]_(m xx n)` is a square matrix, if
The minimum number of zeros in an upper triangular matrix will be ______.
How many matrices can be obtained by using one or more numbers from four given numbers?
If A and B are square matrices of order 3 × 3 and |A| = –1, |B| = 3, then |3AB| equals ______.
Let A and B be 3 × 3 real matrices such that A is symmetric matrix and B is skew-symmetric matrix. Then the systems of linear equations (A2B2 – B2A2)X = O, where X is a 3 × 1 column matrix of unknown variables and O is a 3 × 1 null matrix, has ______.
If A = `[(0, -tan θ/2),(tan θ/2, 0)]` and (I2 + A) (I2 – A)–1 = `[(a, -b),(b, a)]` then 13(a2 + b2) is equal to ______.
If `A = [(1,-1,2),(0,-1,3)], B = [(-2,1),(3,-1),(0,2)],` then AB is a singular matrix.
Assertion: Let the matrices A = `((-3, 2),(-5, 4))` and B = `((4, -2),(5, -3))` be such that A100B = BA100
Reason: AB = BA implies AB = BA for all positive integers n.
