Advertisements
Advertisements
प्रश्न
Use product `[(1,-1,2),(0,2,-3),(3,-2,4)][(-2,0,1),(9,2,-3),(6,1,-2)]` to solve the system of equations x + 3z = 9, −x + 2y − 2z = 4, 2x − 3y + 4z = −3
उत्तर

Since, A × B = I,
∴ B = A−1 .....(1)
Now, the given system of equations is
x + 3z = 9
−x + 2y − 2z = 4
2x − 3y + 4z = −3
This can also be represented as,

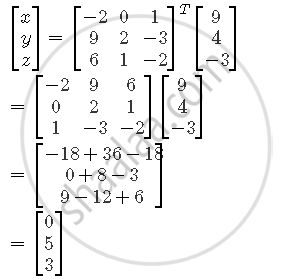
Hence, x = 0, y = 5 and z = 3.
APPEARS IN
संबंधित प्रश्न
if `A = [(3,-4),(1,-1)]` then prove A"=` [(1+2n, -4n),(n, 1-2n)]` where n is any positive integer
In a certain city there are 30 colleges. Each college has 15 peons, 6 clerks, 1 typist and 1 section officer. Express the given information as a column matrix. Using scalar multiplication, find the total number of posts of each kind in all the colleges.
Find the non-singular matrices P & Q such that PAQ is in normal form where`[(1,2,3,4),(2,1,4,3),(3,0,5,-10)]`
If li, mi, ni, i = 1, 2, 3 denote the direction cosines of three mutually perpendicular vectors in space, prove that AAT = I, where \[A = \begin{bmatrix}l_1 & m_1 & n_1 \\ l_2 & m_2 & n_2 \\ l_3 & m_3 & n_3\end{bmatrix}\]
Choose the correct alternative.
The matrix `[(8, 0, 0),(0, 8, 0),(0, 0, 8)]` is _______
Classify the following matrix as, a row, a column, a square, a diagonal, a scalar, a unit, an upper triangular, a lower triangular, a symmetric or a skew-symmetric matrix:
`[9 sqrt(2) -3]`
Classify the following matrix as, a row, a column, a square, a diagonal, a scalar, a unit, an upper triangular, a lower triangular, a symmetric or a skew-symmetric matrix:
`[(2, 0, 0),(3, -1, 0),(-7, 3, 1)]`
Classify the following matrix as, a row, a column, a square, a diagonal, a scalar, a unit, an upper triangular, a lower triangular, a symmetric or a skew-symmetric matrix:
`[(10, -15, 27),(-15, 0, sqrt(34)),(27, sqrt(34), 5/3)]`
Classify the following matrix as, a row, a column, a square, a diagonal, a scalar, a unit, an upper triangular, a lower triangular, a symmetric or a skew-symmetric matrix:
`[(0, 0, 1),(0, 1, 0),(1, 0, 0)]`
Identify the following matrix is singular or non-singular?
`[(5, 0, 5),(1, 99, 100),(6, 99, 105)]`
Find k if the following matrix is singular:
`[(7, 3),(-2, "k")]`
Select the correct option from the given alternatives:
Given A = `[(1, 3),(2, 2)]`, I = `[(1, 0),(0, 1)]` if A – λI is a singular matrix then _______
Answer the following question:
If A = `[(1, 2, 3),(2, 4, 6),(1, 2, 3)]`, B = `[(1, -1, 1),(-3, 2, -1),(-2, 1, 0)]`, show that AB and BA are both singular matrices
Answer the following question:
If A = `[(1, omega),(omega^2, 1)]`, B = `[(omega^2, 1),(1, omega)]`, where ω is a complex cube root of unity, then show that AB + BA + A −2B is a null matrix
Choose the correct alternative:
If B = `[(6, 3),(-2, "k")]` is singular matrix, then the value of k is ______
Show by an example that for A ≠ O, B ≠ O, AB = O
If X and Y are 2 × 2 matrices, then solve the following matrix equations for X and Y.
2X + 3Y = `[(2, 3),(4, 0)]`, 3Y + 2Y = `[(-2, 2),(1, -5)]`
A square matrix A = [aij]nxn is called a diagonal matrix if aij = 0 for ____________.
The matrix `[(0,5,-7),(-5,0,11),(7,-11,0)]` is ____________.
The matrix A `=[(0,1),(1,0)]` is a ____________.
If `[(1,2),(3,4)],` then A2 - 5A is equal to ____________.
A diagonal matrix is said to be a scalar matrix if its diagonal elements are
A square matrix in which elements in the diagonal are all 1 and rest are all zero is called an
The number of all possible matrices of order 3/3, with each entry 0 or 1 is
How many matrices can be obtained by using one or more numbers from four given numbers?
Let A = `[(0, -2),(2, 0)]`. If M and N are two matrices given by M = `sum_(k = 1)^10 A^(2k)` and N = `sum_(k = 1)^10 A^(2k - 1)` then MN2 is ______.
If A = `[(0, -tan θ/2),(tan θ/2, 0)]` and (I2 + A) (I2 – A)–1 = `[(a, -b),(b, a)]` then 13(a2 + b2) is equal to ______.
