Advertisements
Advertisements
प्रश्न
Use product `[(1,-1,2),(0,2,-3),(3,-2,4)][(-2,0,1),(9,2,-3),(6,1,-2)]` to solve the system of equations x + 3z = 9, −x + 2y − 2z = 4, 2x − 3y + 4z = −3
उत्तर

Since, A × B = I,
∴ B = A−1 .....(1)
Now, the given system of equations is
x + 3z = 9
−x + 2y − 2z = 4
2x − 3y + 4z = −3
This can also be represented as,

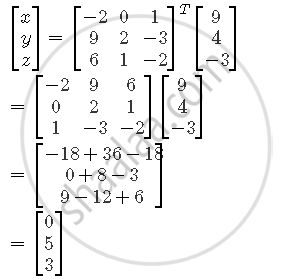
Hence, x = 0, y = 5 and z = 3.
APPEARS IN
संबंधित प्रश्न
If A is a square matrix such that A2 = I, then find the simplified value of (A – I)3 + (A + I)3 – 7A.
If for any 2 x 2 square matrix A, `A("adj" "A") = [(8,0), (0,8)]`, then write the value of |A|
if `A = [(0, -tan alpha/2), (tan alpha/2, 0)]` and I is the identity matrix of order 2, show that I + A = `(I -A)[(cos alpha, -sin alpha),(sin alpha, cos alpha)]`
if A = [(1,1,1),(1,1,1),(1,1,1)], Prove that A" = `[(3^(n-1),3^(n-1),3^(n-1)),(3^(n-1),3^(n-1),3^(n-1)),(3^(n-1),3^(n-1),3^(n-1))]` `n in N`
Find the non-singular matrices P & Q such that PAQ is in normal form where`[(1,2,3,4),(2,1,4,3),(3,0,5,-10)]`
Investigate for what values of λ and μ the equations
2x + 3y + 5z = 9
7x + 3y - 2z = 8
2x + 3y + λz = μ have
A. No solutions
B. Unique solutions
C. An infinite number of solutions.
If li, mi, ni, i = 1, 2, 3 denote the direction cosines of three mutually perpendicular vectors in space, prove that AAT = I, where \[A = \begin{bmatrix}l_1 & m_1 & n_1 \\ l_2 & m_2 & n_2 \\ l_3 & m_3 & n_3\end{bmatrix}\]
If\[A = \begin{bmatrix}2 & 3 \\ 4 & 5\end{bmatrix}\]prove that A − AT is a skew-symmetric matrix.
If A = `[[0 , 2],[3, -4]]` and kA = `[[0 , 3"a"],[2"b", 24]]` then find the value of k,a and b.
if `vec"a"= 2hat"i" + 3hat"j"+ hat"k", vec"b" = hat"i" -2hat"j" + hat"k" and vec"c" = -3hat"i" + hat"j" + 2hat"k", "find" [vec"a" vec"b" vec"c"]`
Classify the following matrix as, a row, a column, a square, a diagonal, a scalar, a unit, an upper triangular, a lower triangular, a symmetric or a skew-symmetric matrix:
`[(3, 0, 0),(0, 5, 0),(0, 0, 1/3)]`
Find k if the following matrix is singular:
`[(4, 3, 1),(7, "k", 1),(10, 9, 1)]`
If A = `[(7, 3, 1),(-2, -4, 1),(5, 9, 1)]`, Find (AT)T.
The following matrix, using its transpose state whether it is symmetric, skew-symmetric, or neither:
`[(2, 5, 1),(-5, 4, 6),(-1, -6, 3)]`
The following matrix, using its transpose state whether it is symmetric, skew-symmetric, or neither:
`[(0, 1 + 2"i", "i" - 2),(-1 - 2"i", 0, -7),(2 - "i", 7, 0)]`
If A = `[(1, 0),(-1, 7)]`, find k so that A2 – 8A – kI = O, where I is a unit matrix and O is a null matrix of order 2.
Select the correct option from the given alternatives:
Given A = `[(1, 3),(2, 2)]`, I = `[(1, 0),(0, 1)]` if A – λI is a singular matrix then _______
Answer the following question:
If A = `[(1, 2),(3, 2),(-1, 0)]` and B = `[(1, 3, 2),(4, -1, -3)]`, show that AB is singular.
If A = `[(6, 0),("p", "q")]` is a scalar matrix, then the values of p and q are ______ respectively.
If A = `[(3, 1),(-1, 2)]`, then prove that A2 – 5A + 7I = O, where I is unit matrix of order 2
If A = `[(1, 3, 3),(3, 1, 3),(3, 3, 1)]`, then show that A2 – 5A is a scalar matrix
If A and B are matrices of same order, then (3A –2B)′ is equal to______.
The matrix A `=[(0,1),(1,0)]` is a ____________.
If a matrix A is both symmetric and skew symmetric then matrix A is ____________.
A matrix is said to be a row matrix, if it has
If all the elements are zero, then matrix is said to be
If D = `[(0, aα^2, aβ^2),(bα + c, 0, aγ^2),(bβ + c, (bγ + c), 0)]` is a skew-symmetric matrix (where α, β, γ are distinct) and the value of `|((a + 1)^2, (1 - a), (2 - c)),((3 + c), (b + 2)^2, (b + 1)^2),((3 - b)^2, b^2, (c + 3))|` is λ then the value of |10λ| is ______.
How many matrices can be obtained by using one or more numbers from four given numbers?
If `[(1, 2, 1),(2, 3, 1),(3, a, 1)]` is non-singular matrix and a ∈ A, then the set A is ______.
If `A = [(1,-1,2),(0,-1,3)], B = [(-2,1),(3,-1),(0,2)],` then AB is a singular matrix.
