Advertisements
Advertisements
प्रश्न
Define the terms (i) half-life (T1/2) and (ii) average life (τ). Find out their relationships with the decay constant (λ).
उत्तर
Half-life
The half-life of a radioactive substance is defined as the average time for which the nuclei of the atoms of the radioactive substance exist.
`t = t_(1/2)`
`R =1/2R_0`
`∴ t_(1/2)=(1n2)/λ`
`=(0.693)/4`
Average life or mean-life (τ):
`tau``=(λN_0int_0^oo te^(-λ1)dt)/N_0`
= `λint_0^oo te^(-λ1)dt`
`tau=1/lambda`
`∴ T_(1/2)=(1n2)/λ = tau 1n2`
संबंधित प्रश्न
Obtain the binding energy of the nuclei `""_26^56"Fe"` and `""_83^209"Bi"` in units of MeV from the following data:
`"m"(""_26^56"Fe")` = 55.934939 u
`"m"(""_83^209"Bi")`= 208.980388 u
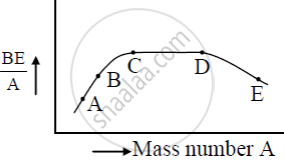
Use this graph to explain the release of energy in both the processes of nuclear fusion and fission.
Which property of nuclear force explains the constancy of binding energy per nucleon `((BE)/A)` for nuclei in the range 20< A < 170 ?
Calculate mass defect and binding energy per nucleon of `"_10^20 Ne`, given
Mass of `"_10^20 Ne= 19.992397` u
Mass of `"_0^1H = 1.007825` u
Mass of `"_0^1n = 1.008665` u
The figure shows the plot of binding energy (BE) per nucleon as a function of mass number A. The letters A, B, C, D, and E represent the positions of typical nuclei on the curve. Point out, giving reasons, the two processes (in terms of A, B, C, D, and E ), one of which can occur due to nuclear fission and the other due to nuclear fusion.
In a periodic table the average atomic mass of magnesium is given as 24.312 u. The average value is based on their relative natural abundance on earth. The three isotopes and their masses are\[\ce{_12^24Mg}\](23.98504 u), \[\ce{_12^25Mg}\] (24.98584 u), and \[\ce{_12^26Mg}\] (25.98259 u). The natural abundance of \[\ce{_12^24Mg}\] is 78.99% by mass. Calculate the abundances of other two isotopes.
Find the binding energy of a H-atom in the state n = 2
Calculate the binding energy of an alpha particle in MeV. Given
mass of a proton = 1.007825 u
mass of a neutron = 1.008665 u
mass of He nucleus = 4.002800 u
1u = 931 MeV/c2
What is binding energy of nucleus?
Find the binding energy per nucleon of 235U based on the information given below.
| Mass(u) | |
| mass of neutral `""_92^235"U"` | 235.0439 |
| mass of a proton | 1.0073 |
| mass of a neutron | 1.0087 |
