Advertisements
Advertisements
प्रश्न
Determine the maximum value of Z = 3x + 4y if the feasible region (shaded) for a LPP is shown in Figure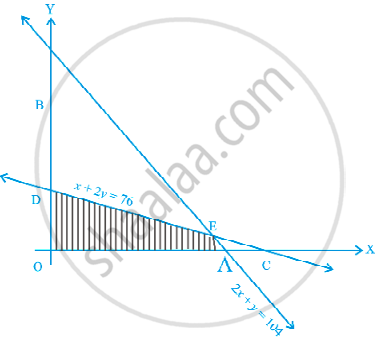
उत्तर
OAED is the feasible region.
At A, y = 0
∴ 2x + y = 104
⇒ x = 52
At D, x = 0
∴ x + 2y = 76
⇒ y = 38
Which gives corner point D = (0, 38)
Now solving the given equations, we get
x + 2y = 76
2x + y = 104
2x + 4y = 152
2x + y = 104
(–) (–) (–)
3y = 48
⇒ y = 16
x + 2(16) = 76
⇒ x = 76 – 32 = 44
So, the corner point E = (44, 16)
Evaluating the maximum value of Z, we get
| Corner points | Z = 3x + 4y | |
| O(0, 0) | Z = 3(0) + 4(0) = 0 | |
| A(52, 0) | Z = 3(52) + 4(0) = 156 | |
| E(44, 16) | Z = 3(44) + 4(16) = 196 | ← Maximum |
| D(0, 38) | Z = 3(0) + 4(38) = 152 |
Hence, the maximum value of Z is 196 at (44, 16).
APPEARS IN
संबंधित प्रश्न
Solve the following Linear Programming Problems graphically:
Maximise Z = 3x + 4y
subject to the constraints : x + y ≤ 4, x ≥ 0, y ≥ 0.
Solve the following Linear Programming Problems graphically:
Maximise Z = 3x + 2y
subject to x + 2y ≤ 10, 3x + y ≤ 15, x, y ≥ 0.
Solve the following Linear Programming Problems graphically:
Minimise Z = x + 2y
subject to 2x + y ≥ 3, x + 2y ≥ 6, x, y ≥ 0.
Show that the minimum of Z occurs at more than two points.
Minimise and Maximise Z = x + 2y
subject to x + 2y ≥ 100, 2x – y ≤ 0, 2x + y ≤ 200; x, y ≥ 0.
Refer to Example 9. How many packets of each food should be used to maximize the amount of vitamin A in the diet? What is the maximum amount of vitamin A in the diet?
An aeroplane can carry a maximum of 200 passengers. A profit of Rs 1000 is made on each executive class ticket and a profit of Rs 600 is made on each economy class ticket. The airline reserves at least 20 seats for executive class. However, at least 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximize the profit for the airline. What is the maximum profit?
If the feasible region for a linear programming problem is bounded, then the objective function Z = ax + by has both a maximum and a minimum value on R.
Maximise the function Z = 11x + 7y, subject to the constraints: x ≤ 3, y ≤ 2, x ≥ 0, y ≥ 0.
Feasible region (shaded) for a LPP is shown in Figure. Maximise Z = 5x + 7y.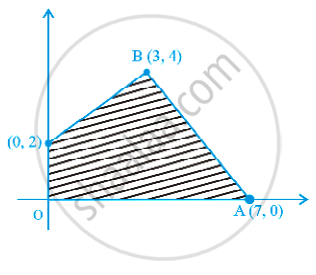
Refer to Exercise 7 above. Find the maximum value of Z.
The feasible region for a LPP is shown in figure. Evaluate Z = 4x + y at each of the corner points of this region. Find the minimum value of Z, if it exists.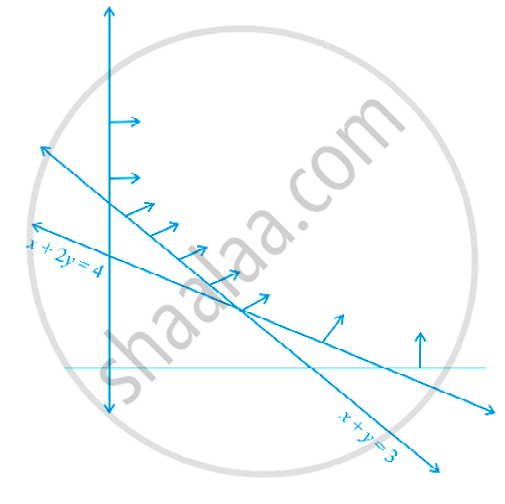
In figure, the feasible region (shaded) for a LPP is shown. Determine the maximum and minimum value of Z = x + 2y.
A man rides his motorcycle at the speed of 50 km/hour. He has to spend Rs 2 per km on petrol. If he rides it at a faster speed of 80 km/hour, the petrol cost increases to Rs 3 per km. He has atmost Rs 120 to spend on petrol and one hour’s time. He wishes to find the maximum distance that he can travel. Express this problem as a linear programming problem
Refer to question 15. Determine the maximum distance that the man can travel.
The corner points of the feasible region determined by the system of linear constraints are (0, 0), (0, 40), (20, 40), (60, 20), (60, 0). The objective function is Z = 4x + 3y ______.
Compare the quantity in Column A and Column B
| Column A | Column B |
| Maximum of Z | 325 |
Corner points of the feasible region for an LPP are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5). Let F = 4x + 6y be the objective function. The Minimum value of F occurs at ______.
In a LPP, the linear inequalities or restrictions on the variables are called ____________.
In a LPP, the objective function is always ______.
If the feasible region for a LPP is unbounded, maximum or minimum of the objective function Z = ax + by may or may not exist.
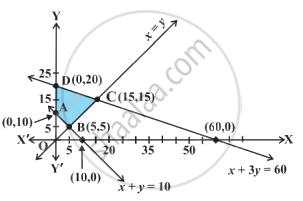
Based on the given shaded region as the feasible region in the graph, at which point(s) is the objective function Z = 3x + 9y maximum?
A linear programming problem is as follows:
Minimize Z = 30x + 50y
Subject to the constraints: 3x + 5y ≥ 15, 2x + 3y ≤ 18, x ≥ 0, y ≥ 0
In the feasible region, the minimum value of Z occurs at:
The maximum value of the object function Z = 5x + 10 y subject to the constraints x + 2y ≤ 120, x + y ≥ 60, x - 2y ≥ 0, x ≥ 0, y ≥ 0 is ____________.
In Corner point method for solving a linear programming problem, one finds the feasible region of the linear programming problem, determines its corner points, and evaluates the objective function Z = ax + by at each corner point. If M and m respectively be the largest and smallest values at corner points then ____________.
Maximize Z = 4x + 6y, subject to 3x + 2y ≤ 12, x + y ≥ 4, x, y ≥ 0.
Maximize Z = 10 x1 + 25 x2, subject to 0 ≤ x1 ≤ 3, 0 ≤ x2 ≤ 3, x1 + x2 ≤ 5.
Maximize Z = 10×1 + 25×2, subject to 0 ≤ x1 ≤ 3, 0 ≤ x2 ≤ 3, x1 + x2 ≤ 5.
