Advertisements
Advertisements
प्रश्न
Determine the maximum value of Z = 3x + 4y if the feasible region (shaded) for a LPP is shown in Figure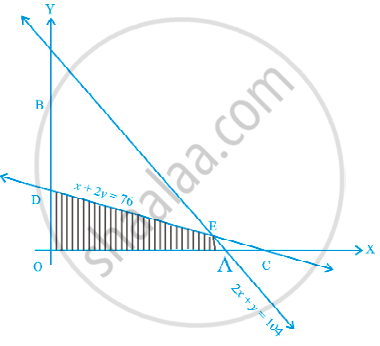
उत्तर
OAED is the feasible region.
At A, y = 0
∴ 2x + y = 104
⇒ x = 52
At D, x = 0
∴ x + 2y = 76
⇒ y = 38
Which gives corner point D = (0, 38)
Now solving the given equations, we get
x + 2y = 76
2x + y = 104
2x + 4y = 152
2x + y = 104
(–) (–) (–)
3y = 48
⇒ y = 16
x + 2(16) = 76
⇒ x = 76 – 32 = 44
So, the corner point E = (44, 16)
Evaluating the maximum value of Z, we get
| Corner points | Z = 3x + 4y | |
| O(0, 0) | Z = 3(0) + 4(0) = 0 | |
| A(52, 0) | Z = 3(52) + 4(0) = 156 | |
| E(44, 16) | Z = 3(44) + 4(16) = 196 | ← Maximum |
| D(0, 38) | Z = 3(0) + 4(38) = 152 |
Hence, the maximum value of Z is 196 at (44, 16).
APPEARS IN
संबंधित प्रश्न
Solve the following Linear Programming Problems graphically:
Maximise Z = 3x + 4y
subject to the constraints : x + y ≤ 4, x ≥ 0, y ≥ 0.
Solve the following Linear Programming Problems graphically:
Minimise Z = 3x + 5y
such that x + 3y ≥ 3, x + y ≥ 2, x, y ≥ 0.
Show that the minimum of Z occurs at more than two points.
Minimise and Maximise Z = 5x + 10 y
subject to x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x, y ≥ 0.
Show that the minimum of Z occurs at more than two points.
Maximise Z = x + y, subject to x – y ≤ –1, –x + y ≤ 0, x, y ≥ 0.
A farmer mixes two brands P and Q of cattle feed. Brand P, costing Rs 250 per bag contains 3 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing Rs 200 per bag contains 1.5 units of nutritional elements A, 11.25 units of element B, and 3 units of element C. The minimum requirements of nutrients A, B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?
A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each toy on the machines is given below:
| Type of toy | Machines | ||
| I | II | III | |
| A | 12 | 18 | 6 |
| B | 6 | 0 | 9 |
Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is Rs 7.50 and that on each toy of type B is Rs 5, show that 15 toys of type A and 30 of type B should be manufactured in a day to get maximum profit.
To maintain his health a person must fulfil certain minimum daily requirements for several kinds of nutrients. Assuming that there are only three kinds of nutrients-calcium, protein and calories and the person's diet consists of only two food items, I and II, whose price and nutrient contents are shown in the table below:
| Food I (per lb) |
Food II (per lb) |
Minimum daily requirement for the nutrient |
||||
| Calcium | 10 | 5 | 20 | |||
| Protein | 5 | 4 | 20 | |||
| Calories | 2 | 6 | 13 | |||
| Price (Rs) | 60 | 100 |
What combination of two food items will satisfy the daily requirement and entail the least cost? Formulate this as a LPP.
Maximise Z = 3x + 4y, subject to the constraints: x + y ≤ 1, x ≥ 0, y ≥ 0
Maximise the function Z = 11x + 7y, subject to the constraints: x ≤ 3, y ≤ 2, x ≥ 0, y ≥ 0.
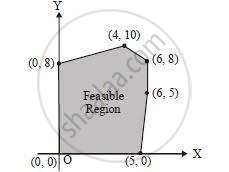
Feasible region (shaded) for a LPP is shown in Figure. Maximise Z = 5x + 7y.
Refer to quastion 12. What will be the minimum cost?
Refer to question 14. How many sweaters of each type should the company make in a day to get a maximum profit? What is the maximum profit.
Maximise Z = x + y subject to x + 4y ≤ 8, 2x + 3y ≤ 12, 3x + y ≤ 9, x ≥ 0, y ≥ 0.
In order to supplement daily diet, a person wishes to take some X and some wishes Y tablets. The contents of iron, calcium and vitamins in X and Y (in milligrams per tablet) are given as below:
| Tablets | Iron | Calcium | Vitamin |
| X | 6 | 3 | 2 |
| Y | 2 | 3 | 4 |
The person needs atleast 18 milligrams of iron, 21 milligrams of calcium and 16 milligrams of vitamin. The price of each tablet of X and Y is Rs 2 and Rs 1 respectively. How many tablets of each should the person take in order to satisfy the above requirement at the minimum cost?
A company makes 3 model of calculators: A, B and C at factory I and factory II. The company has orders for at least 6400 calculators of model A, 4000 calculator of model B and 4800 calculator of model C. At factory I, 50 calculators of model A, 50 of model B and 30 of model C are made every day; at factory II, 40 calculators of model A, 20 of model B and 40 of model C are made everyday. It costs Rs 12000 and Rs 15000 each day to operate factory I and II, respectively. Find the number of days each factory should operate to minimise the operating costs and still meet the demand.
Refer to Question 32, Maximum of F – Minimum of F = ______.
In a LPP, the linear inequalities or restrictions on the variables are called ____________.
In a LPP if the objective function Z = ax + by has the same maximum value on two corner points of the feasible region, then every point on the line segment joining these two points give the same ______ value.
The feasible region for an LPP is always a ______ polygon.
In Corner point method for solving a linear programming problem, one finds the feasible region of the linear programming problem, determines its corner points, and evaluates the objective function Z = ax + by at each corner point. If M and m respectively be the largest and smallest values at corner points then ____________.
Maximize Z = 3x + 5y, subject to x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0.
Maximize Z = 4x + 6y, subject to 3x + 2y ≤ 12, x + y ≥ 4, x, y ≥ 0.
Maximize Z = 10 x1 + 25 x2, subject to 0 ≤ x1 ≤ 3, 0 ≤ x2 ≤ 3, x1 + x2 ≤ 5.
Z = 6x + 21 y, subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0. The minimum value of Z occurs at ____________.
The feasible region for an LPP is shown shaded in the figure. Let Z = 3x - 4y be the objective function. Minimum of Z occurs at ____________.