Advertisements
Advertisements
प्रश्न
To maintain his health a person must fulfil certain minimum daily requirements for several kinds of nutrients. Assuming that there are only three kinds of nutrients-calcium, protein and calories and the person's diet consists of only two food items, I and II, whose price and nutrient contents are shown in the table below:
| Food I (per lb) |
Food II (per lb) |
Minimum daily requirement for the nutrient |
||||
| Calcium | 10 | 5 | 20 | |||
| Protein | 5 | 4 | 20 | |||
| Calories | 2 | 6 | 13 | |||
| Price (Rs) | 60 | 100 |
What combination of two food items will satisfy the daily requirement and entail the least cost? Formulate this as a LPP.
उत्तर
Let the person takes x lbs and y lbs of food I and II respectively that were taken in the diet.
Since, per lb of food I costs Rs 60 and that of food II costs Rs 100.
Therefore, x lbs of food I costs Rs 60x and y lbs of food II costs Rs 100y.
Total cost per day = Rs (60x + 100y)
Let Z denote the total cost per day
Then, Z = 60x + 100y
Total amount of calcium in the diet is \[10x + 5y\]
Since, each lb of food I contains 10 units of calcium.Therefore, x lbs of food I contains 10x units of calcium.
Each lb of food II contains 5 units of calciu.So,y lbs of food II contains 5y units of calcium.
Thus, x lbs of food I and y lbs of food II contains 10x + 5y units of calcium.
But, the minimum requirement is 20 lbs of calcium.
Each lb of food II contains 4 units of protein.So,y lbs of food II contains 4y units of protein.
Thus, x lbs of food I and y lbs of food II contains 5x + 4y units of protein.
But, the minimum requirement is 20 lbs of protein.
Each lb of food II contains units of calories.So,y lbs of food II contains 6y units of calories.
Thus, x lbs of food I and y lbs of food II contains
But, the minimum requirement is 13 lbs of calories.
So,
Min Z = 60x + 100y
subject to
\[5x + 4y \geq 20\]
\[2x + 6y \geq 13\]
\[x, y \geq 0\]
APPEARS IN
संबंधित प्रश्न
Two tailors, A and B, earn Rs 300 and Rs 400 per day respectively. A can stitch 6 shirts and 4 pairs of trousers while B can stitch 10 shirts and 4 pairs of trousers per day. To find how many days should each of them work and if it is desired to produce at least 60 shirts and 32 pairs of trousers at a minimum labour cost, formulate this as an LPP
Solve the following Linear Programming Problems graphically:
Maximise Z = 3x + 4y
subject to the constraints : x + y ≤ 4, x ≥ 0, y ≥ 0.
Solve the following Linear Programming Problems graphically:
Maximise Z = 5x + 3y
subject to 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0
Show that the minimum of Z occurs at more than two points.
Maximise Z = – x + 2y, Subject to the constraints:
x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0.
Show that the minimum of Z occurs at more than two points.
Maximise Z = x + y, subject to x – y ≤ –1, –x + y ≤ 0, x, y ≥ 0.
A farmer mixes two brands P and Q of cattle feed. Brand P, costing Rs 250 per bag contains 3 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing Rs 200 per bag contains 1.5 units of nutritional elements A, 11.25 units of element B, and 3 units of element C. The minimum requirements of nutrients A, B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?
A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each toy on the machines is given below:
| Type of toy | Machines | ||
| I | II | III | |
| A | 12 | 18 | 6 |
| B | 6 | 0 | 9 |
Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is Rs 7.50 and that on each toy of type B is Rs 5, show that 15 toys of type A and 30 of type B should be manufactured in a day to get maximum profit.
If the feasible region for a linear programming problem is bounded, then the objective function Z = ax + by has both a maximum and a minimum value on R.
Determine the maximum value of Z = 11x + 7y subject to the constraints : 2x + y ≤ 6, x ≤ 2, x ≥ 0, y ≥ 0.
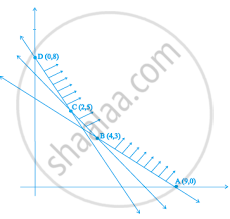
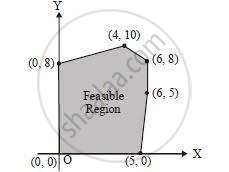
The feasible region for a LPP is shown in Figure. Find the minimum value of Z = 11x + 7y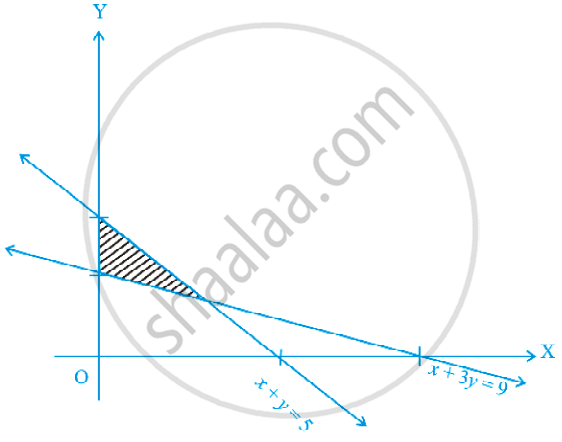
Refer to quastion 12. What will be the minimum cost?
Refer to question 15. Determine the maximum distance that the man can travel.
Refer to Question 27. Maximum of Z occurs at ______.
Refer to Question 27. (Maximum value of Z + Minimum value of Z) is equal to ______.
Refer to Question 32, Maximum of F – Minimum of F = ______.
If the feasible region for a LPP is ______ then the optimal value of the objective function Z = ax + by may or may not exist.
In a LPP if the objective function Z = ax + by has the same maximum value on two corner points of the feasible region, then every point on the line segment joining these two points give the same ______ value.
A feasible region of a system of linear inequalities is said to be ______ if it can be enclosed within a circle.
The feasible region for an LPP is always a ______ polygon.
Maximum value of the objective function Z = ax + by in a LPP always occurs at only one corner point of the feasible region.
Based on the given shaded region as the feasible region in the graph, at which point(s) is the objective function Z = 3x + 9y maximum?
In the given graph, the feasible region for an LPP is shaded. The objective function Z = 2x – 3y will be minimum at:
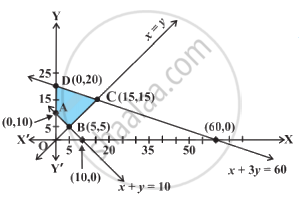
The maximum value of the object function Z = 5x + 10 y subject to the constraints x + 2y ≤ 120, x + y ≥ 60, x - 2y ≥ 0, x ≥ 0, y ≥ 0 is ____________.
In linear programming, optimal solution ____________.
A maximum or a minimum may not exist for a linear programming problem if ____________.
In Corner point method for solving a linear programming problem, one finds the feasible region of the linear programming problem, determines its corner points, and evaluates the objective function Z = ax + by at each corner point. If M and m respectively be the largest and smallest values at corner points then ____________.
In Corner point method for solving a linear programming problem, one finds the feasible region of the linear programming problem, determines its corner points, and evaluates the objective function Z = ax + by at each corner point. Let M and m respectively be the largest and smallest values at corner points. In case the feasible region is unbounded, m is the minimum value of the objective function.
If two corner points of the feasible region are both optimal solutions of the same type, i.e., both produce the same maximum or minimum.
Maximize Z = 7x + 11y, subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0.
Z = 6x + 21 y, subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0. The minimum value of Z occurs at ____________.
The feasible region for an LPP is shown shaded in the figure. Let Z = 3x - 4y be the objective function. Minimum of Z occurs at ____________.
Maximize Z = 10×1 + 25×2, subject to 0 ≤ x1 ≤ 3, 0 ≤ x2 ≤ 3, x1 + x2 ≤ 5.
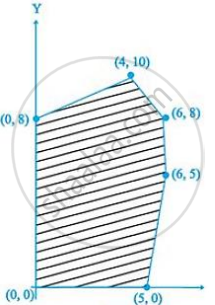
The feasible region for an LPP is shown shaded in the following figure. Minimum of Z = 4x + 3y occurs at the point.