Advertisements
Advertisements
Question
To maintain his health a person must fulfil certain minimum daily requirements for several kinds of nutrients. Assuming that there are only three kinds of nutrients-calcium, protein and calories and the person's diet consists of only two food items, I and II, whose price and nutrient contents are shown in the table below:
| Food I (per lb) |
Food II (per lb) |
Minimum daily requirement for the nutrient |
||||
| Calcium | 10 | 5 | 20 | |||
| Protein | 5 | 4 | 20 | |||
| Calories | 2 | 6 | 13 | |||
| Price (Rs) | 60 | 100 |
What combination of two food items will satisfy the daily requirement and entail the least cost? Formulate this as a LPP.
Solution
Let the person takes x lbs and y lbs of food I and II respectively that were taken in the diet.
Since, per lb of food I costs Rs 60 and that of food II costs Rs 100.
Therefore, x lbs of food I costs Rs 60x and y lbs of food II costs Rs 100y.
Total cost per day = Rs (60x + 100y)
Let Z denote the total cost per day
Then, Z = 60x + 100y
Total amount of calcium in the diet is \[10x + 5y\]
Since, each lb of food I contains 10 units of calcium.Therefore, x lbs of food I contains 10x units of calcium.
Each lb of food II contains 5 units of calciu.So,y lbs of food II contains 5y units of calcium.
Thus, x lbs of food I and y lbs of food II contains 10x + 5y units of calcium.
But, the minimum requirement is 20 lbs of calcium.
Each lb of food II contains 4 units of protein.So,y lbs of food II contains 4y units of protein.
Thus, x lbs of food I and y lbs of food II contains 5x + 4y units of protein.
But, the minimum requirement is 20 lbs of protein.
Each lb of food II contains units of calories.So,y lbs of food II contains 6y units of calories.
Thus, x lbs of food I and y lbs of food II contains
But, the minimum requirement is 13 lbs of calories.
So,
Min Z = 60x + 100y
subject to
\[5x + 4y \geq 20\]
\[2x + 6y \geq 13\]
\[x, y \geq 0\]
APPEARS IN
RELATED QUESTIONS
Solve the following Linear Programming Problems graphically:
Maximise Z = 3x + 2y
subject to x + 2y ≤ 10, 3x + y ≤ 15, x, y ≥ 0.
Solve the following Linear Programming Problems graphically:
Minimise Z = x + 2y
subject to 2x + y ≥ 3, x + 2y ≥ 6, x, y ≥ 0.
Show that the minimum of Z occurs at more than two points.
Minimise and Maximise Z = x + 2y
subject to x + 2y ≥ 100, 2x – y ≤ 0, 2x + y ≤ 200; x, y ≥ 0.
A farmer mixes two brands P and Q of cattle feed. Brand P, costing Rs 250 per bag contains 3 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing Rs 200 per bag contains 1.5 units of nutritional elements A, 11.25 units of element B, and 3 units of element C. The minimum requirements of nutrients A, B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?
The minimum value of the objective function Z = ax + by in a linear programming problem always occurs at only one corner point of the feasible region
Determine the maximum value of Z = 3x + 4y if the feasible region (shaded) for a LPP is shown in Figure
The feasible region for a LPP is shown in Figure. Find the minimum value of Z = 11x + 7y
Refer to quastion 12. What will be the minimum cost?
Refer to question 13. Solve the linear programming problem and determine the maximum profit to the manufacturer
Maximise Z = x + y subject to x + 4y ≤ 8, 2x + 3y ≤ 12, 3x + y ≤ 9, x ≥ 0, y ≥ 0.
A company makes 3 model of calculators: A, B and C at factory I and factory II. The company has orders for at least 6400 calculators of model A, 4000 calculator of model B and 4800 calculator of model C. At factory I, 50 calculators of model A, 50 of model B and 30 of model C are made every day; at factory II, 40 calculators of model A, 20 of model B and 40 of model C are made everyday. It costs Rs 12000 and Rs 15000 each day to operate factory I and II, respectively. Find the number of days each factory should operate to minimise the operating costs and still meet the demand.
The corner points of the feasible region determined by the system of linear constraints are (0, 0), (0, 40), (20, 40), (60, 20), (60, 0). The objective function is Z = 4x + 3y ______.
Compare the quantity in Column A and Column B
| Column A | Column B |
| Maximum of Z | 325 |
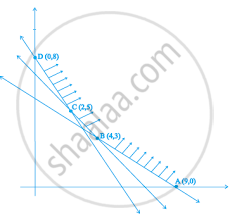
The feasible solution for a LPP is shown in Figure. Let Z = 3x – 4y be the objective function. Minimum of Z occurs at ______.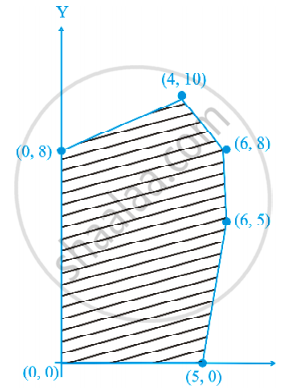
Refer to Question 27. Maximum of Z occurs at ______.
The feasible region for an LPP is shown in the figure. Let F = 3x – 4y be the objective function. Maximum value of F is ______.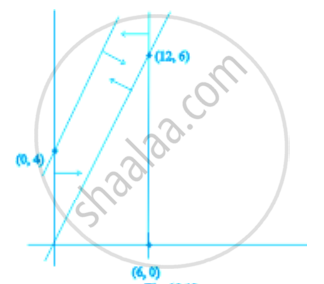
Corner points of the feasible region for an LPP are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5). Let F = 4x + 6y be the objective function. The Minimum value of F occurs at ______.
In a LPP if the objective function Z = ax + by has the same maximum value on two corner points of the feasible region, then every point on the line segment joining these two points give the same ______ value.
A feasible region of a system of linear inequalities is said to be ______ if it can be enclosed within a circle.
A corner point of a feasible region is a point in the region which is the ______ of two boundary lines.
If the feasible region for a LPP is unbounded, maximum or minimum of the objective function Z = ax + by may or may not exist.
Maximum value of the objective function Z = ax + by in a LPP always occurs at only one corner point of the feasible region.
In the given graph, the feasible region for an LPP is shaded. The objective function Z = 2x – 3y will be minimum at:
In a linear programming problem, the constraints on the decision variables x and y are x − 3y ≥ 0, y ≥ 0, 0 ≤ x ≤ 3. The feasible region:
Objective function of a linear programming problem is ____________.
The maximum value of the object function Z = 5x + 10 y subject to the constraints x + 2y ≤ 120, x + y ≥ 60, x - 2y ≥ 0, x ≥ 0, y ≥ 0 is ____________.
Z = 7x + y, subject to 5x + y ≥ 5, x + y ≥ 3, x ≥ 0, y ≥ 0. The minimum value of Z occurs at ____________.
In linear programming infeasible solutions
A maximum or a minimum may not exist for a linear programming problem if ____________.
In Corner point method for solving a linear programming problem, one finds the feasible region of the linear programming problem, determines its corner points, and evaluates the objective function Z = ax + by at each corner point. Let M and m respectively be the largest and smallest values at corner points. In case feasible region is unbounded, M is the maximum value of the objective function if ____________.
Maximize Z = 7x + 11y, subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0.
Maximize Z = 6x + 4y, subject to x ≤ 2, x + y ≤ 3, -2x + y ≤ 1, x ≥ 0, y ≥ 0.
Z = 6x + 21 y, subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0. The minimum value of Z occurs at ____________.
Maximize Z = 10×1 + 25×2, subject to 0 ≤ x1 ≤ 3, 0 ≤ x2 ≤ 3, x1 + x2 ≤ 5.
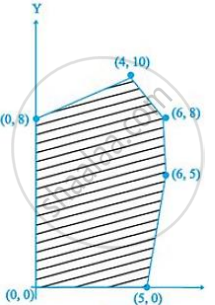
The feasible region for an LPP is shown shaded in the following figure. Minimum of Z = 4x + 3y occurs at the point.