Advertisements
Advertisements
Question
Refer to question 13. Solve the linear programming problem and determine the maximum profit to the manufacturer
Solution
As per the solution of Question No.13
We have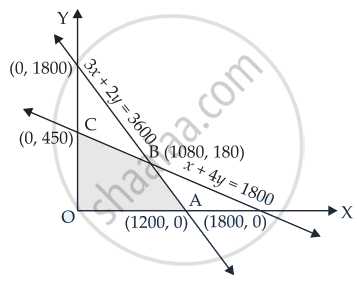
Let 3x + 2y = 3600
| x | 0 | 1200 |
| y | 1800 | 0 |
Let x + 4y = 1800
| x | 0 | 1800 |
| y | 450 | 0 |
Maximise Z = 100x + 170y
Subject to the constraints
3x + 2y ≤ 3600 ......(i)
x + 4y ≤ 1800 .......(ii)
x ≥ 0, y ≥ 0
On solving equation (i) and (ii) we get
x = 1080 and y = 180
OABC is the feasible region whose corner points are O(0, 0), A(1200, 0), B(1080, 180), C(0, 450).
Let us evaluate the value of Z.
| Corner points | Value of Z = 100x + 170y | |
| O(0, 0) | Z = 100(0) + 170(0) = 0 | |
| A(1200, 0) | Z = 100(1200) + 0 = 120000 | |
| B(1080, 180) | Z = 100(1080) + 170(180) = 138600 |
← Maximum |
| C(0, 450) | Z = 170(450) = 76500 |
Hence, the maximum value of Z is 138600 at (1080, 180).
APPEARS IN
RELATED QUESTIONS
Solve the following Linear Programming Problems graphically:
Minimise Z = – 3x + 4 y
subject to x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0.
Solve the following Linear Programming Problems graphically:
Maximise Z = 3x + 2y
subject to x + 2y ≤ 10, 3x + y ≤ 15, x, y ≥ 0.
Solve the following Linear Programming Problems graphically:
Minimise Z = x + 2y
subject to 2x + y ≥ 3, x + 2y ≥ 6, x, y ≥ 0.
Show that the minimum of Z occurs at more than two points.
Maximise Z = – x + 2y, Subject to the constraints:
x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0.
Show that the minimum of Z occurs at more than two points.
Maximise Z = x + y, subject to x – y ≤ –1, –x + y ≤ 0, x, y ≥ 0.
Maximise Z = 3x + 4y, subject to the constraints: x + y ≤ 1, x ≥ 0, y ≥ 0
Determine the maximum value of Z = 3x + 4y if the feasible region (shaded) for a LPP is shown in Figure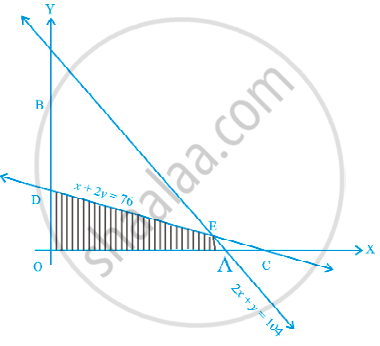
In figure, the feasible region (shaded) for a LPP is shown. Determine the maximum and minimum value of Z = x + 2y.
Refer to question 15. Determine the maximum distance that the man can travel.
Maximise Z = x + y subject to x + 4y ≤ 8, 2x + 3y ≤ 12, 3x + y ≤ 9, x ≥ 0, y ≥ 0.
The feasible solution for a LPP is shown in Figure. Let Z = 3x – 4y be the objective function. Minimum of Z occurs at ______.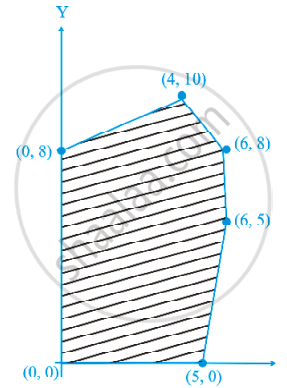
Refer to Question 27. Maximum of Z occurs at ______.
Refer to Question 32, Maximum of F – Minimum of F = ______.
In a LPP, the linear inequalities or restrictions on the variables are called ____________.
If the feasible region for a LPP is unbounded, maximum or minimum of the objective function Z = ax + by may or may not exist.
In a LPP, the minimum value of the objective function Z = ax + by is always 0 if the origin is one of the corner point of the feasible region.
In a LPP, the maximum value of the objective function Z = ax + by is always finite.
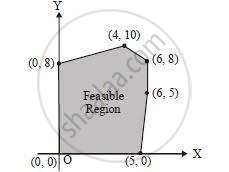
Based on the given shaded region as the feasible region in the graph, at which point(s) is the objective function Z = 3x + 9y maximum?
A linear programming problem is as follows:
Minimize Z = 30x + 50y
Subject to the constraints: 3x + 5y ≥ 15, 2x + 3y ≤ 18, x ≥ 0, y ≥ 0
In the feasible region, the minimum value of Z occurs at:
In a linear programming problem, the constraints on the decision variables x and y are x − 3y ≥ 0, y ≥ 0, 0 ≤ x ≤ 3. The feasible region:
The maximum value of the object function Z = 5x + 10 y subject to the constraints x + 2y ≤ 120, x + y ≥ 60, x - 2y ≥ 0, x ≥ 0, y ≥ 0 is ____________.
A maximum or a minimum may not exist for a linear programming problem if ____________.
In Corner point method for solving a linear programming problem, one finds the feasible region of the linear programming problem, determines its corner points, and evaluates the objective function Z = ax + by at each corner point. If M and m respectively be the largest and smallest values at corner points then ____________.
In Corner point method for solving a linear programming problem, one finds the feasible region of the linear programming problem, determines its corner points, and evaluates the objective function Z = ax + by at each corner point. Let M and m respectively be the largest and smallest values at corner points. In case the feasible region is unbounded, m is the minimum value of the objective function.
If two corner points of the feasible region are both optimal solutions of the same type, i.e., both produce the same maximum or minimum.
Maximize Z = 7x + 11y, subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0.
The feasible region for an LPP is shown shaded in the figure. Let Z = 3x - 4y be the objective function. Minimum of Z occurs at ____________.