Advertisements
Advertisements
प्रश्न
Determine the maximum value of Z = 11x + 7y subject to the constraints : 2x + y ≤ 6, x ≤ 2, x ≥ 0, y ≥ 0.
उत्तर
Given that: Z = 11x + 7y and the constraints 2x + y ≤ 6, x ≤ 2, x ≥ 0, y ≥ 0
Let 2x + y = 6
| x | 0 | 3 |
| y | 6 | 0 |
The shaded area OABC is the feasible region determined by the constraints
2x + y ≤ 6
x ≤ 2
x ≥ 0
y ≥ 0
The feasible region is bounded.
So, maximum value will occur at a corner point of the feasible region.
Corner points are (0, 0), (2, 0), (2, 2) and (0, 6).
Now, evaluating the value of Z, we get
| Corner points | Value of Z | |
| O(0, 0) | 11(0) + 7(0) = 0 | |
| A(2, 0) | 11(2) + 7(0) = 22 | |
| B(2, 2) | 11(2) + 7(2) = 36 | |
| C(0, 6) | 11(0) + 7(6) = 42 | ← Maximum |
Hence, the maximum value of Z is 42 at (0, 6).
APPEARS IN
संबंधित प्रश्न
Show that the minimum of Z occurs at more than two points.
Minimise and Maximise Z = 5x + 10 y
subject to x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x, y ≥ 0.
A small firm manufactures necklaces and bracelets. The total number of necklaces and bracelets that it can handle per day is at most 24. It takes one hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is 16. If the profit on a necklace is Rs 100 and that on a bracelet is Rs 300. Formulate on L.P.P. for finding how many of each should be produced daily to maximize the profit?
It is being given that at least one of each must be produced.
To maintain his health a person must fulfil certain minimum daily requirements for several kinds of nutrients. Assuming that there are only three kinds of nutrients-calcium, protein and calories and the person's diet consists of only two food items, I and II, whose price and nutrient contents are shown in the table below:
| Food I (per lb) |
Food II (per lb) |
Minimum daily requirement for the nutrient |
||||
| Calcium | 10 | 5 | 20 | |||
| Protein | 5 | 4 | 20 | |||
| Calories | 2 | 6 | 13 | |||
| Price (Rs) | 60 | 100 |
What combination of two food items will satisfy the daily requirement and entail the least cost? Formulate this as a LPP.
Maximise Z = 3x + 4y, subject to the constraints: x + y ≤ 1, x ≥ 0, y ≥ 0
Maximise the function Z = 11x + 7y, subject to the constraints: x ≤ 3, y ≤ 2, x ≥ 0, y ≥ 0.
Feasible region (shaded) for a LPP is shown in Figure. Maximise Z = 5x + 7y.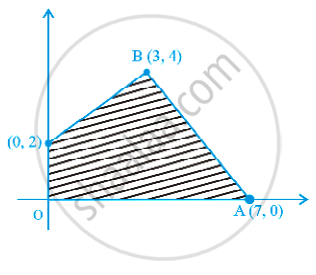
The feasible region for a LPP is shown in Figure. Find the minimum value of Z = 11x + 7y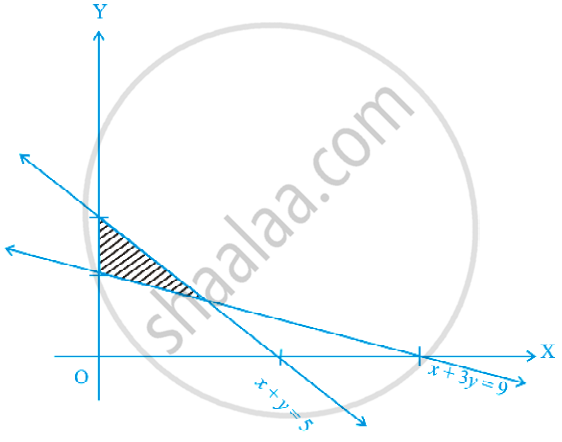
Refer to question 13. Solve the linear programming problem and determine the maximum profit to the manufacturer
Refer to question 14. How many sweaters of each type should the company make in a day to get a maximum profit? What is the maximum profit.
Refer to question 15. Determine the maximum distance that the man can travel.
Maximise Z = x + y subject to x + 4y ≤ 8, 2x + 3y ≤ 12, 3x + y ≤ 9, x ≥ 0, y ≥ 0.
Refer to Question 27. Maximum of Z occurs at ______.
In a LPP, the linear inequalities or restrictions on the variables are called ____________.
In a LPP, the objective function is always ______.
In a LPP if the objective function Z = ax + by has the same maximum value on two corner points of the feasible region, then every point on the line segment joining these two points give the same ______ value.
A linear programming problem is one that is concerned with ____________.
In linear programming infeasible solutions
In linear programming, optimal solution ____________.
A maximum or a minimum may not exist for a linear programming problem if ____________.
In Corner point method for solving a linear programming problem, one finds the feasible region of the linear programming problem, determines its corner points, and evaluates the objective function Z = ax + by at each corner point. If M and m respectively be the largest and smallest values at corner points then ____________.
In a LPP, the objective function is always ____________.
Maximize Z = 7x + 11y, subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0.
Maximize Z = 6x + 4y, subject to x ≤ 2, x + y ≤ 3, -2x + y ≤ 1, x ≥ 0, y ≥ 0.
Maximize Z = 10 x1 + 25 x2, subject to 0 ≤ x1 ≤ 3, 0 ≤ x2 ≤ 3, x1 + x2 ≤ 5.
Z = 6x + 21 y, subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0. The minimum value of Z occurs at ____________.
Maximize Z = 10×1 + 25×2, subject to 0 ≤ x1 ≤ 3, 0 ≤ x2 ≤ 3, x1 + x2 ≤ 5.
