Advertisements
Advertisements
Question
Determine the maximum value of Z = 11x + 7y subject to the constraints : 2x + y ≤ 6, x ≤ 2, x ≥ 0, y ≥ 0.
Solution
Given that: Z = 11x + 7y and the constraints 2x + y ≤ 6, x ≤ 2, x ≥ 0, y ≥ 0
Let 2x + y = 6
| x | 0 | 3 |
| y | 6 | 0 |
The shaded area OABC is the feasible region determined by the constraints
2x + y ≤ 6
x ≤ 2
x ≥ 0
y ≥ 0
The feasible region is bounded.
So, maximum value will occur at a corner point of the feasible region.
Corner points are (0, 0), (2, 0), (2, 2) and (0, 6).
Now, evaluating the value of Z, we get
| Corner points | Value of Z | |
| O(0, 0) | 11(0) + 7(0) = 0 | |
| A(2, 0) | 11(2) + 7(0) = 22 | |
| B(2, 2) | 11(2) + 7(2) = 36 | |
| C(0, 6) | 11(0) + 7(6) = 42 | ← Maximum |
Hence, the maximum value of Z is 42 at (0, 6).
APPEARS IN
RELATED QUESTIONS
Solve the following Linear Programming Problems graphically:
Maximise Z = 3x + 4y
subject to the constraints : x + y ≤ 4, x ≥ 0, y ≥ 0.
Solve the following Linear Programming Problems graphically:
Maximise Z = 5x + 3y
subject to 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0
Show that the minimum of Z occurs at more than two points.
Minimise and Maximise Z = x + 2y
subject to x + 2y ≥ 100, 2x – y ≤ 0, 2x + y ≤ 200; x, y ≥ 0.
Refer to Example 9. How many packets of each food should be used to maximize the amount of vitamin A in the diet? What is the maximum amount of vitamin A in the diet?
A farmer mixes two brands P and Q of cattle feed. Brand P, costing Rs 250 per bag contains 3 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing Rs 200 per bag contains 1.5 units of nutritional elements A, 11.25 units of element B, and 3 units of element C. The minimum requirements of nutrients A, B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?
A dietician wishes to mix together two kinds of food X and Y in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C. The vitamin content of one kg food is given below:
| Food | Vitamin A | Vitamin B | Vitamin C |
| X | 1 | 2 | 3 |
| Y | 2 | 2 | 1 |
One kg of food X costs Rs 16 and one kg of food Y costs Rs 20. Find the least cost of the mixture which will produce the required diet?
If the feasible region for a linear programming problem is bounded, then the objective function Z = ax + by has both a maximum and a minimum value on R.
The minimum value of the objective function Z = ax + by in a linear programming problem always occurs at only one corner point of the feasible region
Maximise the function Z = 11x + 7y, subject to the constraints: x ≤ 3, y ≤ 2, x ≥ 0, y ≥ 0.
Minimise Z = 13x – 15y subject to the constraints: x + y ≤ 7, 2x – 3y + 6 ≥ 0, x ≥ 0, y ≥ 0
In figure, the feasible region (shaded) for a LPP is shown. Determine the maximum and minimum value of Z = x + 2y.
Refer to question 15. Determine the maximum distance that the man can travel.
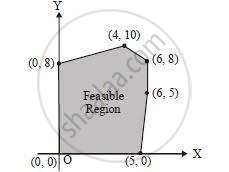
The feasible solution for a LPP is shown in Figure. Let Z = 3x – 4y be the objective function. Minimum of Z occurs at ______.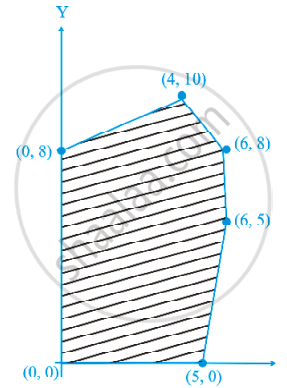
Refer to Question 32, Maximum of F – Minimum of F = ______.
In a LPP if the objective function Z = ax + by has the same maximum value on two corner points of the feasible region, then every point on the line segment joining these two points give the same ______ value.
If the feasible region for a LPP is unbounded, maximum or minimum of the objective function Z = ax + by may or may not exist.
Objective function of a linear programming problem is ____________.
In linear programming infeasible solutions
In linear programming, optimal solution ____________.
A maximum or a minimum may not exist for a linear programming problem if ____________.
In Corner point method for solving a linear programming problem, one finds the feasible region of the linear programming problem, determines its corner points, and evaluates the objective function Z = ax + by at each corner point. If M and m respectively be the largest and smallest values at corner points then ____________.
In a LPP, the objective function is always ____________.
Maximize Z = 3x + 5y, subject to x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0.
Maximize Z = 7x + 11y, subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0.
Maximize Z = 6x + 4y, subject to x ≤ 2, x + y ≤ 3, -2x + y ≤ 1, x ≥ 0, y ≥ 0.
The feasible region for an LPP is shown shaded in the figure. Let Z = 3x - 4y be the objective function. Minimum of Z occurs at ____________.