Advertisements
Advertisements
Question
Refer to question 15. Determine the maximum distance that the man can travel.
Solution
Referring to the solution of Question No.15, we have
Maximise Z = x + y subject to the constraints
Let 2x + 3y = 120
| x | 0 | 60 |
| y | 40 | 0 |
Let 8x + 5y = 400
| x | 0 | 50 |
| y | 80 | 0 |
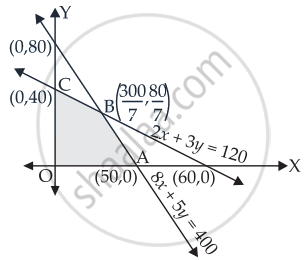
2x + 3y ≤ 120 ......(i)
8x + 5y ≤ 400 ......(ii)
x ≥ 0, y ≥ 0
On solving eq. (i) and (ii) we get
x = `300/7` and y = `80/7`
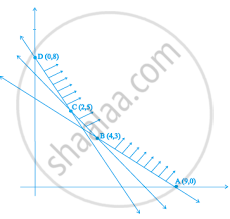
Here, OABC is the feasible region whose corner points are O(0, 0), A(50, 0), `"B"(300/7, 80/7)` and C(0, 40).
Let us evaluate the value of Z
| Corner points | Value of Z = x + y | |
| O(0, 0) | Z = 0 + 0 = 0 | |
| A(50, 0) | Z = 50 + 0 = 50 km | |
| `"B"(300/7, 80/7)` |
Z = `300/7 + 80/7` = `380/7` = 54.3 km |
← Maximum |
| C(0, 40) | Z = 0 + 40 = 40 km |
Hence, the maximum distance that the man can travel is `54 2/7` km at `(300/7, 80/7)`.
APPEARS IN
RELATED QUESTIONS
Solve the following Linear Programming Problems graphically:
Minimise Z = – 3x + 4 y
subject to x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0.
Solve the following Linear Programming Problems graphically:
Maximise Z = 5x + 3y
subject to 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0
Solve the following Linear Programming Problems graphically:
Maximise Z = 3x + 2y
subject to x + 2y ≤ 10, 3x + y ≤ 15, x, y ≥ 0.
Show that the minimum of Z occurs at more than two points.
Minimise and Maximise Z = 5x + 10 y
subject to x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x, y ≥ 0.
Show that the minimum of Z occurs at more than two points.
Maximise Z = – x + 2y, Subject to the constraints:
x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0.
A farmer mixes two brands P and Q of cattle feed. Brand P, costing Rs 250 per bag contains 3 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing Rs 200 per bag contains 1.5 units of nutritional elements A, 11.25 units of element B, and 3 units of element C. The minimum requirements of nutrients A, B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?
Minimise Z = 13x – 15y subject to the constraints: x + y ≤ 7, 2x – 3y + 6 ≥ 0, x ≥ 0, y ≥ 0
Refer to Exercise 7 above. Find the maximum value of Z.
Refer to question 13. Solve the linear programming problem and determine the maximum profit to the manufacturer
Refer to question 15. Determine the maximum distance that the man can travel.
The corner points of the feasible region determined by the system of linear constraints are (0, 0), (0, 40), (20, 40), (60, 20), (60, 0). The objective function is Z = 4x + 3y ______.
Compare the quantity in Column A and Column B
| Column A | Column B |
| Maximum of Z | 325 |
The feasible solution for a LPP is shown in Figure. Let Z = 3x – 4y be the objective function. Minimum of Z occurs at ______.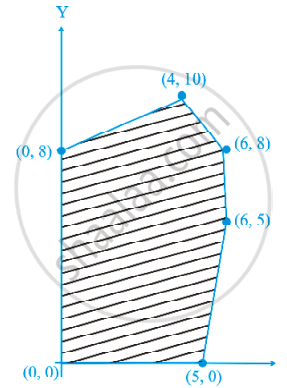
Refer to Question 27. (Maximum value of Z + Minimum value of Z) is equal to ______.
Corner points of the feasible region for an LPP are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5). Let F = 4x + 6y be the objective function. The Minimum value of F occurs at ______.
Refer to Question 32, Maximum of F – Minimum of F = ______.
If the feasible region for a LPP is ______ then the optimal value of the objective function Z = ax + by may or may not exist.
A corner point of a feasible region is a point in the region which is the ______ of two boundary lines.
The feasible region for an LPP is always a ______ polygon.
In the given graph, the feasible region for an LPP is shaded. The objective function Z = 2x – 3y will be minimum at:
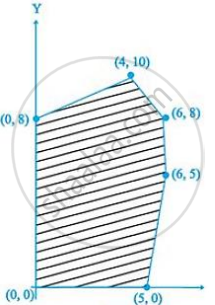
In linear programming, optimal solution ____________.
In a LPP, the objective function is always ____________.
Maximize Z = 6x + 4y, subject to x ≤ 2, x + y ≤ 3, -2x + y ≤ 1, x ≥ 0, y ≥ 0.
Z = 6x + 21 y, subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0. The minimum value of Z occurs at ____________.
The feasible region for an LPP is shown shaded in the following figure. Minimum of Z = 4x + 3y occurs at the point.