Advertisements
Advertisements
प्रश्न
Show that the minimum of Z occurs at more than two points.
Minimise and Maximise Z = 5x + 10 y
subject to x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x, y ≥ 0.
उत्तर
The system of constraints is:
x + 2y ≤ 120 ...(i)
x + y ≥ 60 ....(ii)
x - 2y ≥ 0 ....(iii)
and x, y ≥ 0 ....(iv)
Let l1 : x + 2y = 120
l2 : x + y = 60
l3 : x - 2y = 0
It is observed that the feasible region CADE is bounded.
The coordinates of C, A, D, E are (60, 0), (120, 0), (60, 30), (40, 20) respectively.
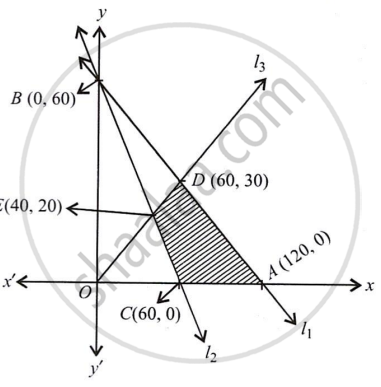
Thus, we use the Corner Point Method to determine the maximum and minimum values of Z.
We have : Z = 5x + l0y
| Corner Point | Corresponding values of Z |
| (60, 0) | 300 (Minimum) |
| (120, 0) | 600 |
| (60, 30) | 600 |
| (40, 20) | 400 |
Hence Zmin = 300 at (60, 0) and Zmax = 600 at all points on the line segment joining the points (120, 0) and (60, 30).
APPEARS IN
संबंधित प्रश्न
Solve the following Linear Programming Problems graphically:
Maximise Z = 5x + 3y
subject to 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0
Solve the following Linear Programming Problems graphically:
Maximise Z = 3x + 2y
subject to x + 2y ≤ 10, 3x + y ≤ 15, x, y ≥ 0.
Solve the following Linear Programming Problems graphically:
Minimise Z = x + 2y
subject to 2x + y ≥ 3, x + 2y ≥ 6, x, y ≥ 0.
Show that the minimum of Z occurs at more than two points.
Minimise and Maximise Z = x + 2y
subject to x + 2y ≥ 100, 2x – y ≤ 0, 2x + y ≤ 200; x, y ≥ 0.
Refer to Example 9. How many packets of each food should be used to maximize the amount of vitamin A in the diet? What is the maximum amount of vitamin A in the diet?
An aeroplane can carry a maximum of 200 passengers. A profit of Rs 1000 is made on each executive class ticket and a profit of Rs 600 is made on each economy class ticket. The airline reserves at least 20 seats for executive class. However, at least 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximize the profit for the airline. What is the maximum profit?
The minimum value of the objective function Z = ax + by in a linear programming problem always occurs at only one corner point of the feasible region
Maximise Z = 3x + 4y, subject to the constraints: x + y ≤ 1, x ≥ 0, y ≥ 0
Minimise Z = 13x – 15y subject to the constraints: x + y ≤ 7, 2x – 3y + 6 ≥ 0, x ≥ 0, y ≥ 0
Determine the maximum value of Z = 3x + 4y if the feasible region (shaded) for a LPP is shown in Figure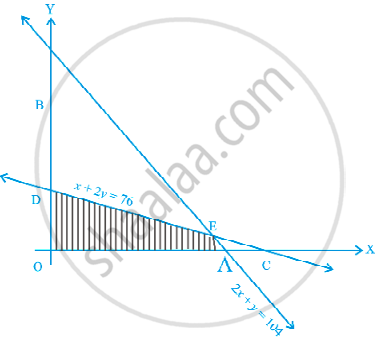
The feasible region for a LPP is shown in figure. Evaluate Z = 4x + y at each of the corner points of this region. Find the minimum value of Z, if it exists.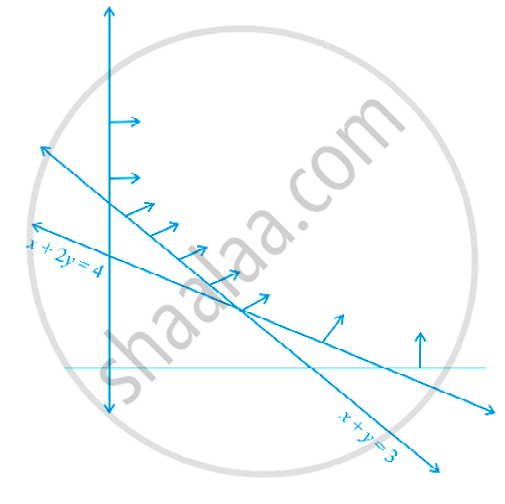
Refer to quastion 12. What will be the minimum cost?
Refer to question 15. Determine the maximum distance that the man can travel.
A manufacturer produces two Models of bikes-Model X and Model Y. Model X takes a 6 man-hours to make per unit, while Model Y takes 10 man-hours per unit. There is a total of 450 man-hour available per week. Handling and Marketing costs are Rs 2000 and Rs 1000 per unit for Models X and Y respectively. The total funds available for these purposes are Rs 80,000 per week. Profits per unit for Models X and Y are Rs 1000 and Rs 500, respectively. How many bikes of each model should the manufacturer produce so as to yield a maximum profit? Find the maximum profit.
A company makes 3 model of calculators: A, B and C at factory I and factory II. The company has orders for at least 6400 calculators of model A, 4000 calculator of model B and 4800 calculator of model C. At factory I, 50 calculators of model A, 50 of model B and 30 of model C are made every day; at factory II, 40 calculators of model A, 20 of model B and 40 of model C are made everyday. It costs Rs 12000 and Rs 15000 each day to operate factory I and II, respectively. Find the number of days each factory should operate to minimise the operating costs and still meet the demand.
The feasible solution for a LPP is shown in Figure. Let Z = 3x – 4y be the objective function. Minimum of Z occurs at ______.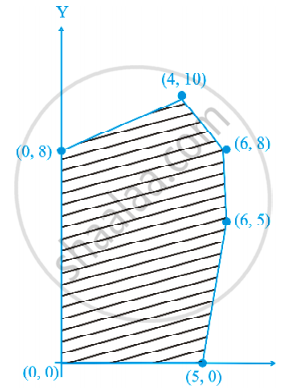
The feasible region for an LPP is shown in the figure. Let F = 3x – 4y be the objective function. Maximum value of F is ______.
Refer to Question 30. Minimum value of F is ______.
Corner points of the feasible region for an LPP are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5). Let F = 4x + 6y be the objective function. The Minimum value of F occurs at ______.
Refer to Question 32, Maximum of F – Minimum of F = ______.
If the feasible region for a LPP is ______ then the optimal value of the objective function Z = ax + by may or may not exist.
The feasible region for an LPP is always a ______ polygon.
If the feasible region for a LPP is unbounded, maximum or minimum of the objective function Z = ax + by may or may not exist.
In a LPP, the minimum value of the objective function Z = ax + by is always 0 if the origin is one of the corner point of the feasible region.
Based on the given shaded region as the feasible region in the graph, at which point(s) is the objective function Z = 3x + 9y maximum?
A linear programming problem is as follows:
Minimize Z = 30x + 50y
Subject to the constraints: 3x + 5y ≥ 15, 2x + 3y ≤ 18, x ≥ 0, y ≥ 0
In the feasible region, the minimum value of Z occurs at:
For an objective function Z = ax + by, where a, b > 0; the corner points of the feasible region determined by a set of constraints (linear inequalities) are (0, 20), (10, 10), (30, 30) and (0, 40). The condition on a and b such that the maximum Z occurs at both the points (30, 30) and (0, 40) is:
Objective function of a linear programming problem is ____________.
The maximum value of the object function Z = 5x + 10 y subject to the constraints x + 2y ≤ 120, x + y ≥ 60, x - 2y ≥ 0, x ≥ 0, y ≥ 0 is ____________.
In Corner point method for solving a linear programming problem, one finds the feasible region of the linear programming problem, determines its corner points, and evaluates the objective function Z = ax + by at each corner point. If M and m respectively be the largest and smallest values at corner points then ____________.
In Corner point method for solving a linear programming problem, one finds the feasible region of the linear programming problem, determines its corner points, and evaluates the objective function Z = ax + by at each corner point. Let M and m respectively be the largest and smallest values at corner points. In case feasible region is unbounded, M is the maximum value of the objective function if ____________.
Maximize Z = 10 x1 + 25 x2, subject to 0 ≤ x1 ≤ 3, 0 ≤ x2 ≤ 3, x1 + x2 ≤ 5.
Z = 6x + 21 y, subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0. The minimum value of Z occurs at ____________.
