Advertisements
Advertisements
प्रश्न
Solve the following Linear Programming Problems graphically:
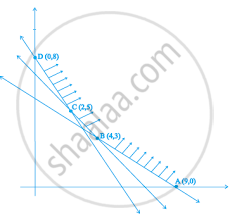
Maximise Z = 5x + 3y
subject to 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0
उत्तर
The system of constraints is:
3x + 5y ≤ 15 ....(i)
5x + 2y ≤ 10 ...(ii)
and x ≥ 0, y ≥ 0 ...(iii)
Let l1: 3x + 5y = 15
l2: 5x + 2y = 10
The shaded region in the figure is the feasible region determined by the system of constraints (i) to (iii)
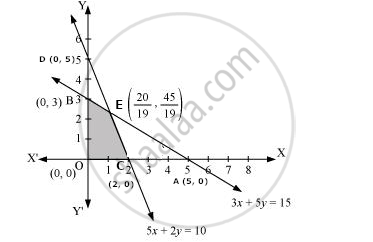
It is observed that the feasible region OCEB is bounded.
Thus, we use the corner point Method to determine the maximum value of Z.
We have: Z = 5x + 3x
The co-ordinates if O,C.E and B are (0, 0) (2, 0), `(20/19, 45/19)`
(on solving 3x + 5y = 15, 5x + 2y = 10) and (0, 3) respectively.
| Corner point | Corresponding values of Z |
| (2, 0) | 10 |
| `(20/19, 45/19)` | `235/19` (Maximum) |
| (0, 3) | 9 |
| (0, 0) | 0 |
Hence, `Z_(max) = 235/19 "at" (20/19, 45/19)`
APPEARS IN
संबंधित प्रश्न
Two tailors, A and B, earn Rs 300 and Rs 400 per day respectively. A can stitch 6 shirts and 4 pairs of trousers while B can stitch 10 shirts and 4 pairs of trousers per day. To find how many days should each of them work and if it is desired to produce at least 60 shirts and 32 pairs of trousers at a minimum labour cost, formulate this as an LPP
Show that the minimum of Z occurs at more than two points.
Maximise Z = x + y, subject to x – y ≤ –1, –x + y ≤ 0, x, y ≥ 0.
A dietician wishes to mix together two kinds of food X and Y in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C. The vitamin content of one kg food is given below:
| Food | Vitamin A | Vitamin B | Vitamin C |
| X | 1 | 2 | 3 |
| Y | 2 | 2 | 1 |
One kg of food X costs Rs 16 and one kg of food Y costs Rs 20. Find the least cost of the mixture which will produce the required diet?
A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each toy on the machines is given below:
| Type of toy | Machines | ||
| I | II | III | |
| A | 12 | 18 | 6 |
| B | 6 | 0 | 9 |
Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is Rs 7.50 and that on each toy of type B is Rs 5, show that 15 toys of type A and 30 of type B should be manufactured in a day to get maximum profit.
Maximise the function Z = 11x + 7y, subject to the constraints: x ≤ 3, y ≤ 2, x ≥ 0, y ≥ 0.
Minimise Z = 13x – 15y subject to the constraints: x + y ≤ 7, 2x – 3y + 6 ≥ 0, x ≥ 0, y ≥ 0
The feasible region for a LPP is shown in Figure. Find the minimum value of Z = 11x + 7y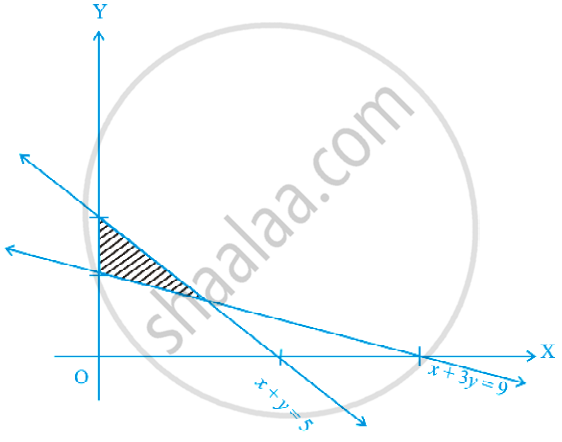
In figure, the feasible region (shaded) for a LPP is shown. Determine the maximum and minimum value of Z = x + 2y.
Refer to question 14. How many sweaters of each type should the company make in a day to get a maximum profit? What is the maximum profit.
A company makes 3 model of calculators: A, B and C at factory I and factory II. The company has orders for at least 6400 calculators of model A, 4000 calculator of model B and 4800 calculator of model C. At factory I, 50 calculators of model A, 50 of model B and 30 of model C are made every day; at factory II, 40 calculators of model A, 20 of model B and 40 of model C are made everyday. It costs Rs 12000 and Rs 15000 each day to operate factory I and II, respectively. Find the number of days each factory should operate to minimise the operating costs and still meet the demand.
The corner points of the feasible region determined by the system of linear constraints are (0, 0), (0, 40), (20, 40), (60, 20), (60, 0). The objective function is Z = 4x + 3y ______.
Compare the quantity in Column A and Column B
| Column A | Column B |
| Maximum of Z | 325 |
Refer to Question 27. Maximum of Z occurs at ______.
Refer to Question 27. (Maximum value of Z + Minimum value of Z) is equal to ______.
The feasible region for an LPP is shown in the figure. Let F = 3x – 4y be the objective function. Maximum value of F is ______.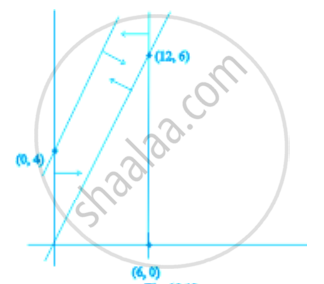
Refer to Question 30. Minimum value of F is ______.
Corner points of the feasible region for an LPP are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5). Let F = 4x + 6y be the objective function. The Minimum value of F occurs at ______.
Refer to Question 32, Maximum of F – Minimum of F = ______.
If the feasible region for a LPP is ______ then the optimal value of the objective function Z = ax + by may or may not exist.
In a LPP if the objective function Z = ax + by has the same maximum value on two corner points of the feasible region, then every point on the line segment joining these two points give the same ______ value.
The feasible region for an LPP is always a ______ polygon.
In a LPP, the maximum value of the objective function Z = ax + by is always finite.
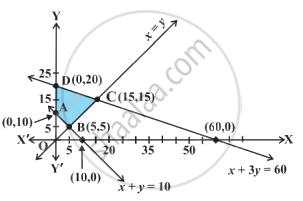
Based on the given shaded region as the feasible region in the graph, at which point(s) is the objective function Z = 3x + 9y maximum?
A linear programming problem is as follows:
Minimize Z = 30x + 50y
Subject to the constraints: 3x + 5y ≥ 15, 2x + 3y ≤ 18, x ≥ 0, y ≥ 0
In the feasible region, the minimum value of Z occurs at:
For an objective function Z = ax + by, where a, b > 0; the corner points of the feasible region determined by a set of constraints (linear inequalities) are (0, 20), (10, 10), (30, 30) and (0, 40). The condition on a and b such that the maximum Z occurs at both the points (30, 30) and (0, 40) is:
In a linear programming problem, the constraints on the decision variables x and y are x − 3y ≥ 0, y ≥ 0, 0 ≤ x ≤ 3. The feasible region:
Objective function of a linear programming problem is ____________.
The maximum value of the object function Z = 5x + 10 y subject to the constraints x + 2y ≤ 120, x + y ≥ 60, x - 2y ≥ 0, x ≥ 0, y ≥ 0 is ____________.
Z = 7x + y, subject to 5x + y ≥ 5, x + y ≥ 3, x ≥ 0, y ≥ 0. The minimum value of Z occurs at ____________.
A linear programming problem is one that is concerned with ____________.
In linear programming, optimal solution ____________.
In Corner point method for solving a linear programming problem, one finds the feasible region of the linear programming problem, determines its corner points, and evaluates the objective function Z = ax + by at each corner point. If M and m respectively be the largest and smallest values at corner points then ____________.
Maximize Z = 3x + 5y, subject to x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0.
Maximize Z = 6x + 4y, subject to x ≤ 2, x + y ≤ 3, -2x + y ≤ 1, x ≥ 0, y ≥ 0.
Maximize Z = 10 x1 + 25 x2, subject to 0 ≤ x1 ≤ 3, 0 ≤ x2 ≤ 3, x1 + x2 ≤ 5.
Z = 6x + 21 y, subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0. The minimum value of Z occurs at ____________.
The feasible region for an LPP is shown shaded in the figure. Let Z = 3x - 4y be the objective function. Minimum of Z occurs at ____________.
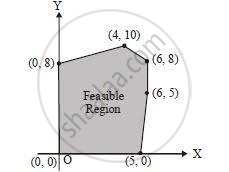
Maximize Z = 10×1 + 25×2, subject to 0 ≤ x1 ≤ 3, 0 ≤ x2 ≤ 3, x1 + x2 ≤ 5.
The feasible region for an LPP is shown shaded in the following figure. Minimum of Z = 4x + 3y occurs at the point.