Advertisements
Advertisements
प्रश्न
The corner points of the feasible region determined by the system of linear constraints are (0, 0), (0, 40), (20, 40), (60, 20), (60, 0). The objective function is Z = 4x + 3y ______.
Compare the quantity in Column A and Column B
| Column A | Column B |
| Maximum of Z | 325 |
विकल्प
The quantity in column A is greater
The quantity in column B is greater
The two quantities are equal
The relationship can not be determined on the basis of the information supplied
उत्तर
The corner points of the feasible region determined by the system of linear constraints are (0, 0), (0, 40), (20, 40), (60, 20), (60, 0). The objective function is Z = 4x + 3y the quantity in column B is greater.
Compare the quantity in Column A and Column B
| Column A | Column B |
| Maximum of Z | 325 |
Explanation:
| Corner points | Value of Z = 4x + 3y | |
| (0, 0) | Z = 0 | |
| (0, 40) | Z = 0 + 3(40) = 120 | |
| (20, 40) | Z = 4(20) + 3(40) = 200 | |
| (60, 20) | Z = 4(60) + 3(20) = 300 | → Maximum |
| (60, 0) | Z = 4(60) + 3(0) = 240 |
APPEARS IN
संबंधित प्रश्न
Solve the following Linear Programming Problems graphically:
Maximise Z = 3x + 4y
subject to the constraints : x + y ≤ 4, x ≥ 0, y ≥ 0.
Solve the following Linear Programming Problems graphically:
Minimise Z = x + 2y
subject to 2x + y ≥ 3, x + 2y ≥ 6, x, y ≥ 0.
Show that the minimum of Z occurs at more than two points.
Minimise and Maximise Z = x + 2y
subject to x + 2y ≥ 100, 2x – y ≤ 0, 2x + y ≤ 200; x, y ≥ 0.
Show that the minimum of Z occurs at more than two points.
Maximise Z = – x + 2y, Subject to the constraints:
x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0.
A small firm manufactures necklaces and bracelets. The total number of necklaces and bracelets that it can handle per day is at most 24. It takes one hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is 16. If the profit on a necklace is Rs 100 and that on a bracelet is Rs 300. Formulate on L.P.P. for finding how many of each should be produced daily to maximize the profit?
It is being given that at least one of each must be produced.
Maximise Z = 3x + 4y, subject to the constraints: x + y ≤ 1, x ≥ 0, y ≥ 0
Maximise the function Z = 11x + 7y, subject to the constraints: x ≤ 3, y ≤ 2, x ≥ 0, y ≥ 0.
Minimise Z = 13x – 15y subject to the constraints: x + y ≤ 7, 2x – 3y + 6 ≥ 0, x ≥ 0, y ≥ 0
In figure, the feasible region (shaded) for a LPP is shown. Determine the maximum and minimum value of Z = x + 2y.
A man rides his motorcycle at the speed of 50 km/hour. He has to spend Rs 2 per km on petrol. If he rides it at a faster speed of 80 km/hour, the petrol cost increases to Rs 3 per km. He has atmost Rs 120 to spend on petrol and one hour’s time. He wishes to find the maximum distance that he can travel. Express this problem as a linear programming problem
Refer to question 14. How many sweaters of each type should the company make in a day to get a maximum profit? What is the maximum profit.
A manufacturer produces two Models of bikes-Model X and Model Y. Model X takes a 6 man-hours to make per unit, while Model Y takes 10 man-hours per unit. There is a total of 450 man-hour available per week. Handling and Marketing costs are Rs 2000 and Rs 1000 per unit for Models X and Y respectively. The total funds available for these purposes are Rs 80,000 per week. Profits per unit for Models X and Y are Rs 1000 and Rs 500, respectively. How many bikes of each model should the manufacturer produce so as to yield a maximum profit? Find the maximum profit.
A company makes 3 model of calculators: A, B and C at factory I and factory II. The company has orders for at least 6400 calculators of model A, 4000 calculator of model B and 4800 calculator of model C. At factory I, 50 calculators of model A, 50 of model B and 30 of model C are made every day; at factory II, 40 calculators of model A, 20 of model B and 40 of model C are made everyday. It costs Rs 12000 and Rs 15000 each day to operate factory I and II, respectively. Find the number of days each factory should operate to minimise the operating costs and still meet the demand.
Refer to Question 27. (Maximum value of Z + Minimum value of Z) is equal to ______.
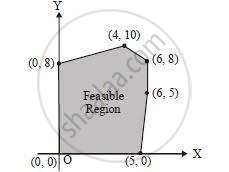
The feasible region for an LPP is shown in the figure. Let F = 3x – 4y be the objective function. Maximum value of F is ______.
The feasible region for an LPP is always a ______ polygon.
Maximum value of the objective function Z = ax + by in a LPP always occurs at only one corner point of the feasible region.
In a LPP, the minimum value of the objective function Z = ax + by is always 0 if the origin is one of the corner point of the feasible region.
Based on the given shaded region as the feasible region in the graph, at which point(s) is the objective function Z = 3x + 9y maximum?
In a linear programming problem, the constraints on the decision variables x and y are x − 3y ≥ 0, y ≥ 0, 0 ≤ x ≤ 3. The feasible region:
Z = 7x + y, subject to 5x + y ≥ 5, x + y ≥ 3, x ≥ 0, y ≥ 0. The minimum value of Z occurs at ____________.
If two corner points of the feasible region are both optimal solutions of the same type, i.e., both produce the same maximum or minimum.
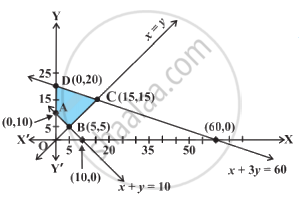
The feasible region for an LPP is shown shaded in the figure. Let Z = 3x - 4y be the objective function. Minimum of Z occurs at ____________.