Advertisements
Advertisements
प्रश्न
Solve the following Linear Programming Problems graphically:
Minimise Z = 3x + 5y
such that x + 3y ≥ 3, x + y ≥ 2, x, y ≥ 0.
उत्तर
The system of constraints is:
x + 3y ≥ 3 ....(i)
x + y ≥ 2 ....(ii)
and x, y ≥ 0 ....(iii)
Let l1 : x + 3y = 3
l2 : x + y = 2
The shaded region in the figure is the feasible region determined by the system of constraints (i) to (iii).
The feasible region is unbounded.
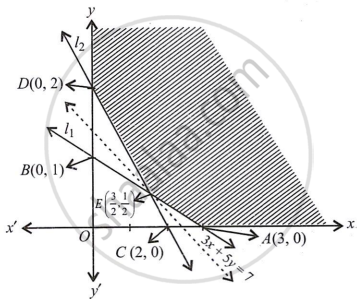
We use the corner point method to determine the minimum value of Z,
We have,
Z = 3x + 5y
The co-ordinated of A, E and D are (3, 0), `(3/2, 1/2).`
(on solving x + 3y = 3 and x + y = 2) and (0, 2) respectively.
We evaluate Z at each corner point
| Corner point | Corresponding value of Z |
| (3, 0) | 9 |
| `(3/2, 1/2)` | 7 (Minimum) |
| (0, 2) | 10 |
Now, Since the region is unbounded we need to check whether 7 is the minimum value or not. To decide this, we graph the inequality 3x + 5y < 7.
Now, in the graph, we observe that 7 does not have points in common with a feasible region.
So, 7 is the minimum value at Z.
Hence, Zmin = 7 at `(3/2, 1/2)`
APPEARS IN
संबंधित प्रश्न
Solve the following Linear Programming Problems graphically:
Maximise Z = 5x + 3y
subject to 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0
Solve the following Linear Programming Problems graphically:
Maximise Z = 3x + 2y
subject to x + 2y ≤ 10, 3x + y ≤ 15, x, y ≥ 0.
Solve the following Linear Programming Problems graphically:
Minimise Z = x + 2y
subject to 2x + y ≥ 3, x + 2y ≥ 6, x, y ≥ 0.
Show that the minimum of Z occurs at more than two points.
Maximise Z = x + y, subject to x – y ≤ –1, –x + y ≤ 0, x, y ≥ 0.
A dietician wishes to mix together two kinds of food X and Y in such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin C. The vitamin content of one kg food is given below:
| Food | Vitamin A | Vitamin B | Vitamin C |
| X | 1 | 2 | 3 |
| Y | 2 | 2 | 1 |
One kg of food X costs Rs 16 and one kg of food Y costs Rs 20. Find the least cost of the mixture which will produce the required diet?
A small firm manufactures necklaces and bracelets. The total number of necklaces and bracelets that it can handle per day is at most 24. It takes one hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is 16. If the profit on a necklace is Rs 100 and that on a bracelet is Rs 300. Formulate on L.P.P. for finding how many of each should be produced daily to maximize the profit?
It is being given that at least one of each must be produced.
To maintain his health a person must fulfil certain minimum daily requirements for several kinds of nutrients. Assuming that there are only three kinds of nutrients-calcium, protein and calories and the person's diet consists of only two food items, I and II, whose price and nutrient contents are shown in the table below:
| Food I (per lb) |
Food II (per lb) |
Minimum daily requirement for the nutrient |
||||
| Calcium | 10 | 5 | 20 | |||
| Protein | 5 | 4 | 20 | |||
| Calories | 2 | 6 | 13 | |||
| Price (Rs) | 60 | 100 |
What combination of two food items will satisfy the daily requirement and entail the least cost? Formulate this as a LPP.
Determine the maximum value of Z = 11x + 7y subject to the constraints : 2x + y ≤ 6, x ≤ 2, x ≥ 0, y ≥ 0.
Minimise Z = 13x – 15y subject to the constraints: x + y ≤ 7, 2x – 3y + 6 ≥ 0, x ≥ 0, y ≥ 0
Determine the maximum value of Z = 3x + 4y if the feasible region (shaded) for a LPP is shown in Figure
Refer to Exercise 7 above. Find the maximum value of Z.
Refer to question 13. Solve the linear programming problem and determine the maximum profit to the manufacturer
Refer to question 15. Determine the maximum distance that the man can travel.
Maximise Z = x + y subject to x + 4y ≤ 8, 2x + 3y ≤ 12, 3x + y ≤ 9, x ≥ 0, y ≥ 0.
A manufacturer produces two Models of bikes-Model X and Model Y. Model X takes a 6 man-hours to make per unit, while Model Y takes 10 man-hours per unit. There is a total of 450 man-hour available per week. Handling and Marketing costs are Rs 2000 and Rs 1000 per unit for Models X and Y respectively. The total funds available for these purposes are Rs 80,000 per week. Profits per unit for Models X and Y are Rs 1000 and Rs 500, respectively. How many bikes of each model should the manufacturer produce so as to yield a maximum profit? Find the maximum profit.
In order to supplement daily diet, a person wishes to take some X and some wishes Y tablets. The contents of iron, calcium and vitamins in X and Y (in milligrams per tablet) are given as below:
| Tablets | Iron | Calcium | Vitamin |
| X | 6 | 3 | 2 |
| Y | 2 | 3 | 4 |
The person needs atleast 18 milligrams of iron, 21 milligrams of calcium and 16 milligrams of vitamin. The price of each tablet of X and Y is Rs 2 and Rs 1 respectively. How many tablets of each should the person take in order to satisfy the above requirement at the minimum cost?
A company makes 3 model of calculators: A, B and C at factory I and factory II. The company has orders for at least 6400 calculators of model A, 4000 calculator of model B and 4800 calculator of model C. At factory I, 50 calculators of model A, 50 of model B and 30 of model C are made every day; at factory II, 40 calculators of model A, 20 of model B and 40 of model C are made everyday. It costs Rs 12000 and Rs 15000 each day to operate factory I and II, respectively. Find the number of days each factory should operate to minimise the operating costs and still meet the demand.
Refer to Question 27. Maximum of Z occurs at ______.
Refer to Question 27. (Maximum value of Z + Minimum value of Z) is equal to ______.
In a LPP, the objective function is always ______.
If the feasible region for a LPP is ______ then the optimal value of the objective function Z = ax + by may or may not exist.
A feasible region of a system of linear inequalities is said to be ______ if it can be enclosed within a circle.
A corner point of a feasible region is a point in the region which is the ______ of two boundary lines.
If the feasible region for a LPP is unbounded, maximum or minimum of the objective function Z = ax + by may or may not exist.
Maximum value of the objective function Z = ax + by in a LPP always occurs at only one corner point of the feasible region.
In a LPP, the minimum value of the objective function Z = ax + by is always 0 if the origin is one of the corner point of the feasible region.
In the given graph, the feasible region for an LPP is shaded. The objective function Z = 2x – 3y will be minimum at:
A linear programming problem is as follows:
Minimize Z = 30x + 50y
Subject to the constraints: 3x + 5y ≥ 15, 2x + 3y ≤ 18, x ≥ 0, y ≥ 0
In the feasible region, the minimum value of Z occurs at:
For an objective function Z = ax + by, where a, b > 0; the corner points of the feasible region determined by a set of constraints (linear inequalities) are (0, 20), (10, 10), (30, 30) and (0, 40). The condition on a and b such that the maximum Z occurs at both the points (30, 30) and (0, 40) is:
A linear programming problem is one that is concerned with ____________.
In linear programming, optimal solution ____________.
In Corner point method for solving a linear programming problem, one finds the feasible region of the linear programming problem, determines its corner points, and evaluates the objective function Z = ax + by at each corner point. If M and m respectively be the largest and smallest values at corner points then ____________.
In Corner point method for solving a linear programming problem, one finds the feasible region of the linear programming problem, determines its corner points, and evaluates the objective function Z = ax + by at each corner point. Let M and m respectively be the largest and smallest values at corner points. In case feasible region is unbounded, M is the maximum value of the objective function if ____________.
If two corner points of the feasible region are both optimal solutions of the same type, i.e., both produce the same maximum or minimum.
Maximize Z = 6x + 4y, subject to x ≤ 2, x + y ≤ 3, -2x + y ≤ 1, x ≥ 0, y ≥ 0.
