Advertisements
Advertisements
प्रश्न
Solve the following Linear Programming Problems graphically:
Minimise Z = 3x + 5y
such that x + 3y ≥ 3, x + y ≥ 2, x, y ≥ 0.
उत्तर
The system of constraints is:
x + 3y ≥ 3 ....(i)
x + y ≥ 2 ....(ii)
and x, y ≥ 0 ....(iii)
Let l1 : x + 3y = 3
l2 : x + y = 2
The shaded region in the figure is the feasible region determined by the system of constraints (i) to (iii).
The feasible region is unbounded.
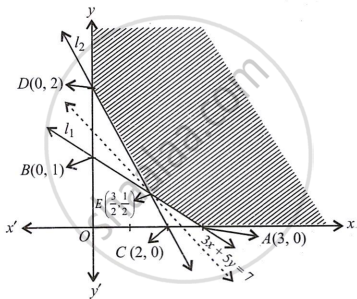
We use the corner point method to determine the minimum value of Z,
We have,
Z = 3x + 5y
The co-ordinated of A, E and D are (3, 0), `(3/2, 1/2).`
(on solving x + 3y = 3 and x + y = 2) and (0, 2) respectively.
We evaluate Z at each corner point
| Corner point | Corresponding value of Z |
| (3, 0) | 9 |
| `(3/2, 1/2)` | 7 (Minimum) |
| (0, 2) | 10 |
Now, Since the region is unbounded we need to check whether 7 is the minimum value or not. To decide this, we graph the inequality 3x + 5y < 7.
Now, in the graph, we observe that 7 does not have points in common with a feasible region.
So, 7 is the minimum value at Z.
Hence, Zmin = 7 at `(3/2, 1/2)`
APPEARS IN
संबंधित प्रश्न
Solve the following Linear Programming Problems graphically:
Maximise Z = 5x + 3y
subject to 3x + 5y ≤ 15, 5x + 2y ≤ 10, x ≥ 0, y ≥ 0
Solve the following Linear Programming Problems graphically:
Minimise Z = x + 2y
subject to 2x + y ≥ 3, x + 2y ≥ 6, x, y ≥ 0.
Show that the minimum of Z occurs at more than two points.
Minimise and Maximise Z = x + 2y
subject to x + 2y ≥ 100, 2x – y ≤ 0, 2x + y ≤ 200; x, y ≥ 0.
A farmer mixes two brands P and Q of cattle feed. Brand P, costing Rs 250 per bag contains 3 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing Rs 200 per bag contains 1.5 units of nutritional elements A, 11.25 units of element B, and 3 units of element C. The minimum requirements of nutrients A, B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag?
A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each toy on the machines is given below:
| Type of toy | Machines | ||
| I | II | III | |
| A | 12 | 18 | 6 |
| B | 6 | 0 | 9 |
Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is Rs 7.50 and that on each toy of type B is Rs 5, show that 15 toys of type A and 30 of type B should be manufactured in a day to get maximum profit.
An aeroplane can carry a maximum of 200 passengers. A profit of Rs 1000 is made on each executive class ticket and a profit of Rs 600 is made on each economy class ticket. The airline reserves at least 20 seats for executive class. However, at least 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximize the profit for the airline. What is the maximum profit?
A small firm manufactures necklaces and bracelets. The total number of necklaces and bracelets that it can handle per day is at most 24. It takes one hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is 16. If the profit on a necklace is Rs 100 and that on a bracelet is Rs 300. Formulate on L.P.P. for finding how many of each should be produced daily to maximize the profit?
It is being given that at least one of each must be produced.
The minimum value of the objective function Z = ax + by in a linear programming problem always occurs at only one corner point of the feasible region
Maximise Z = 3x + 4y, subject to the constraints: x + y ≤ 1, x ≥ 0, y ≥ 0
The feasible region for a LPP is shown in Figure. Find the minimum value of Z = 11x + 7y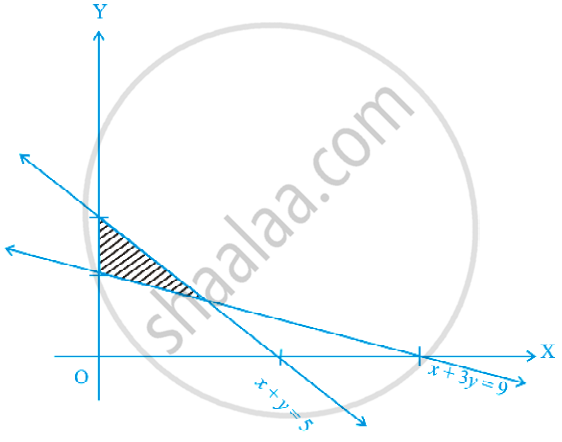
Refer to Exercise 7 above. Find the maximum value of Z.
The feasible region for a LPP is shown in figure. Evaluate Z = 4x + y at each of the corner points of this region. Find the minimum value of Z, if it exists.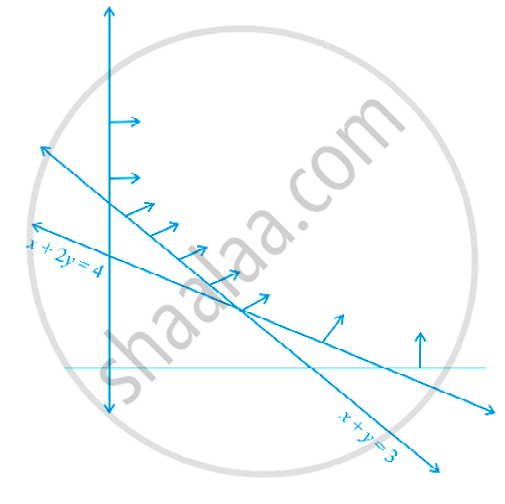
Refer to question 14. How many sweaters of each type should the company make in a day to get a maximum profit? What is the maximum profit.
Refer to question 15. Determine the maximum distance that the man can travel.
Maximise Z = x + y subject to x + 4y ≤ 8, 2x + 3y ≤ 12, 3x + y ≤ 9, x ≥ 0, y ≥ 0.
The feasible solution for a LPP is shown in Figure. Let Z = 3x – 4y be the objective function. Minimum of Z occurs at ______.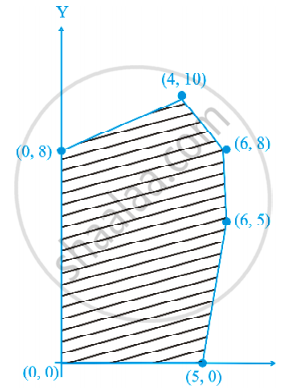
Refer to Question 27. Maximum of Z occurs at ______.
In a LPP, the objective function is always ______.
A corner point of a feasible region is a point in the region which is the ______ of two boundary lines.
Maximum value of the objective function Z = ax + by in a LPP always occurs at only one corner point of the feasible region.
In the given graph, the feasible region for an LPP is shaded. The objective function Z = 2x – 3y will be minimum at:
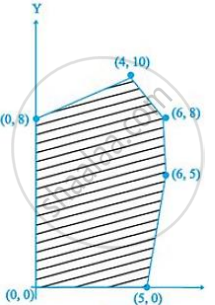
For an objective function Z = ax + by, where a, b > 0; the corner points of the feasible region determined by a set of constraints (linear inequalities) are (0, 20), (10, 10), (30, 30) and (0, 40). The condition on a and b such that the maximum Z occurs at both the points (30, 30) and (0, 40) is:
Objective function of a linear programming problem is ____________.
Z = 7x + y, subject to 5x + y ≥ 5, x + y ≥ 3, x ≥ 0, y ≥ 0. The minimum value of Z occurs at ____________.
A linear programming problem is one that is concerned with ____________.
In linear programming infeasible solutions
In linear programming, optimal solution ____________.
In Corner point method for solving a linear programming problem, one finds the feasible region of the linear programming problem, determines its corner points, and evaluates the objective function Z = ax + by at each corner point. Let M and m respectively be the largest and smallest values at corner points. In case feasible region is unbounded, M is the maximum value of the objective function if ____________.
In Corner point method for solving a linear programming problem, one finds the feasible region of the linear programming problem, determines its corner points, and evaluates the objective function Z = ax + by at each corner point. Let M and m respectively be the largest and smallest values at corner points. In case the feasible region is unbounded, m is the minimum value of the objective function.
If two corner points of the feasible region are both optimal solutions of the same type, i.e., both produce the same maximum or minimum.
Maximize Z = 3x + 5y, subject to x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0.
Maximize Z = 4x + 6y, subject to 3x + 2y ≤ 12, x + y ≥ 4, x, y ≥ 0.
Maximize Z = 10 x1 + 25 x2, subject to 0 ≤ x1 ≤ 3, 0 ≤ x2 ≤ 3, x1 + x2 ≤ 5.
Z = 6x + 21 y, subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0. The minimum value of Z occurs at ____________.
