Advertisements
Advertisements
प्रश्न
Refer to question 15. Determine the maximum distance that the man can travel.
उत्तर
Referring to the solution of Question No.15, we have
Maximise Z = x + y subject to the constraints
Let 2x + 3y = 120
| x | 0 | 60 |
| y | 40 | 0 |
Let 8x + 5y = 400
| x | 0 | 50 |
| y | 80 | 0 |
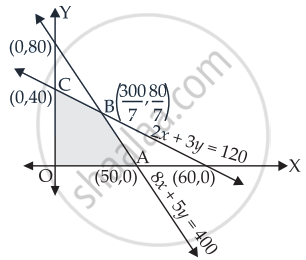
2x + 3y ≤ 120 ......(i)
8x + 5y ≤ 400 ......(ii)
x ≥ 0, y ≥ 0
On solving eq. (i) and (ii) we get
x = `300/7` and y = `80/7`
Here, OABC is the feasible region whose corner points are O(0, 0), A(50, 0), `"B"(300/7, 80/7)` and C(0, 40).
Let us evaluate the value of Z
| Corner points | Value of Z = x + y | |
| O(0, 0) | Z = 0 + 0 = 0 | |
| A(50, 0) | Z = 50 + 0 = 50 km | |
| `"B"(300/7, 80/7)` |
Z = `300/7 + 80/7` = `380/7` = 54.3 km |
← Maximum |
| C(0, 40) | Z = 0 + 40 = 40 km |
Hence, the maximum distance that the man can travel is `54 2/7` km at `(300/7, 80/7)`.
APPEARS IN
संबंधित प्रश्न
Solve the following Linear Programming Problems graphically:
Maximise Z = 3x + 2y
subject to x + 2y ≤ 10, 3x + y ≤ 15, x, y ≥ 0.
Show that the minimum of Z occurs at more than two points.
Maximise Z = – x + 2y, Subject to the constraints:
x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0.
A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each toy on the machines is given below:
| Type of toy | Machines | ||
| I | II | III | |
| A | 12 | 18 | 6 |
| B | 6 | 0 | 9 |
Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is Rs 7.50 and that on each toy of type B is Rs 5, show that 15 toys of type A and 30 of type B should be manufactured in a day to get maximum profit.
If the feasible region for a linear programming problem is bounded, then the objective function Z = ax + by has both a maximum and a minimum value on R.
Maximise Z = 3x + 4y, subject to the constraints: x + y ≤ 1, x ≥ 0, y ≥ 0
Determine the maximum value of Z = 3x + 4y if the feasible region (shaded) for a LPP is shown in Figure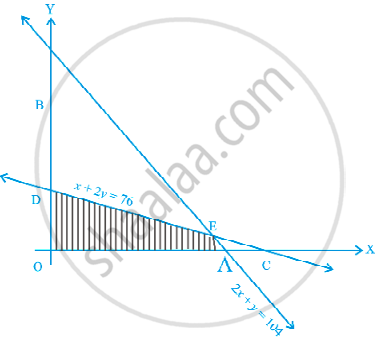
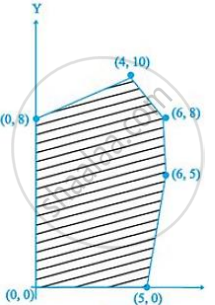
The feasible region for a LPP is shown in figure. Evaluate Z = 4x + y at each of the corner points of this region. Find the minimum value of Z, if it exists.
A man rides his motorcycle at the speed of 50 km/hour. He has to spend Rs 2 per km on petrol. If he rides it at a faster speed of 80 km/hour, the petrol cost increases to Rs 3 per km. He has atmost Rs 120 to spend on petrol and one hour’s time. He wishes to find the maximum distance that he can travel. Express this problem as a linear programming problem
The corner points of the feasible region determined by the system of linear constraints are (0, 0), (0, 40), (20, 40), (60, 20), (60, 0). The objective function is Z = 4x + 3y ______.
Compare the quantity in Column A and Column B
| Column A | Column B |
| Maximum of Z | 325 |
Corner points of the feasible region for an LPP are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5). Let F = 4x + 6y be the objective function. The Minimum value of F occurs at ______.
Refer to Question 32, Maximum of F – Minimum of F = ______.
In a LPP, the linear inequalities or restrictions on the variables are called ____________.
If the feasible region for a LPP is ______ then the optimal value of the objective function Z = ax + by may or may not exist.
In a LPP if the objective function Z = ax + by has the same maximum value on two corner points of the feasible region, then every point on the line segment joining these two points give the same ______ value.
In a LPP, the minimum value of the objective function Z = ax + by is always 0 if the origin is one of the corner point of the feasible region.
In the given graph, the feasible region for an LPP is shaded. The objective function Z = 2x – 3y will be minimum at:
A linear programming problem is as follows:
Minimize Z = 30x + 50y
Subject to the constraints: 3x + 5y ≥ 15, 2x + 3y ≤ 18, x ≥ 0, y ≥ 0
In the feasible region, the minimum value of Z occurs at:
The maximum value of the object function Z = 5x + 10 y subject to the constraints x + 2y ≤ 120, x + y ≥ 60, x - 2y ≥ 0, x ≥ 0, y ≥ 0 is ____________.
In linear programming infeasible solutions
In linear programming, optimal solution ____________.
A maximum or a minimum may not exist for a linear programming problem if ____________.
In a LPP, the objective function is always ____________.
Maximize Z = 3x + 5y, subject to x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0.
Maximize Z = 6x + 4y, subject to x ≤ 2, x + y ≤ 3, -2x + y ≤ 1, x ≥ 0, y ≥ 0.
Maximize Z = 10 x1 + 25 x2, subject to 0 ≤ x1 ≤ 3, 0 ≤ x2 ≤ 3, x1 + x2 ≤ 5.
Z = 6x + 21 y, subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0. The minimum value of Z occurs at ____________.
