Advertisements
Advertisements
प्रश्न
Draw a histogram from the following frequency distribution and find the mode from the graph:
| Class | 0-5 | 5-10 | 10-15 | 15-20 | 20-25 | 25-30 |
| Frequency | 2 | 5 | 18 | 14 | 8 | 5 |
उत्तर १
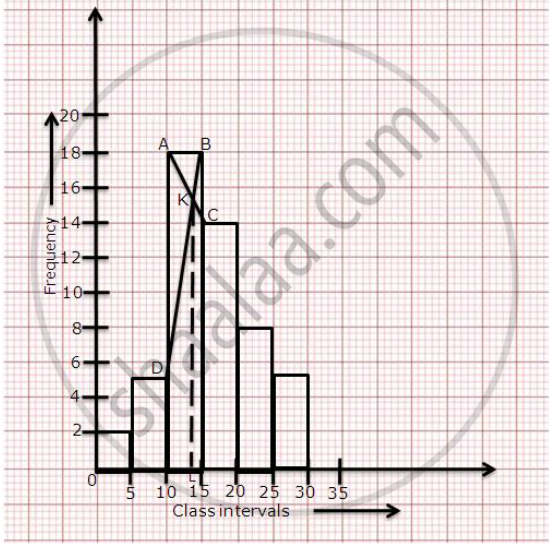
Steps for calculation of mode.
(1) Mark the endpoints of the upper corner of the rectangle with maximum frequency
as A and B.
(2) Mark the inner corner of adjacent rectangles as C and D.
(3) Join AC and BD to intersect at K. From K, draw KL perpendicular to the x-axis.
(4) The value of L on the x-axis represents the mode. Thus, Mode = 13
उत्तर २
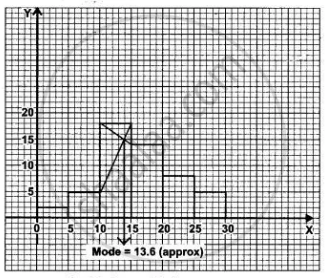
Mode = 13·6
APPEARS IN
संबंधित प्रश्न
The mean of the following distribution is 52 and the frequency of class interval 30-40 is ‘f’. Find ‘f’.
| Class Interval | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 |
| Frequency | 5 | 3 | f | 7 | 2 | 6 | 13 |
The mean of the number 6, ‘y’, 7, ‘x’ and 14 is 8. Express ‘y’ in terms of ‘x’.
Find the mode of following data, using a histogram:
| Class | 0 – 10 | 10 – 20 | 20 – 30 | 30 – 40 | 40 – 50 |
| Frequency | 5 | 12 | 20 | 9 | 4 |
The mean of 1, 7, 5, 3, 4 and 4 is m. The numbers 3, 2, 4, 2, 3, 3 and p have mean m – 1 and median q. Find p and q.
The weights of 11 students in a class are 36 kg, 45 kg, 44 kg, 37 kg, 36 kg, 41 kg, 45 kg, 43 kg, 39 kg, 42 kg and 40 kg. Find the median of their weights.
The mean of a certain number of observations is 32. Find the resulting mean, if the observation is, decreased by 7
Find the median of 18, 19, 20, 23, 22, 20, 17, 19, 25 and 21
Find the mean of: first five odd natural numbers
The mean of five positive integers is twice their median. If four of the integers are 3, 4, 6, 9 and median is 6, then find the fifth integer
The median class for the given distribution is:
| Class Interval | 1 - 5 | 6 - 10 | 11 - 15 | 16 - 20 |
| Cumulative Frequency | 2 | 6 | 11 | 18 |
