Advertisements
Advertisements
प्रश्न
एक त्रिभुज ABC बनाइए जिसमें BC = 6 सेमी, AB = 5 सेमी और ∠ABC = 60 हो। फिर एक त्रिभुज की रचना कीजिए जिसकी भुजाएँ ΔABC की संगत भुजाओं की `3/4` गुनी हों। औचित्य बताइए
Advertisements
उत्तर
∠B = 45°, ∠A = 105°
किसी त्रिभुज के सभी अंतः कोणों का योग 180° होता है।
∠A + ∠B + ∠C = 180°
105° + 45° + ∠C = 180°
∠C = 180° − 150°
∠C = 30°
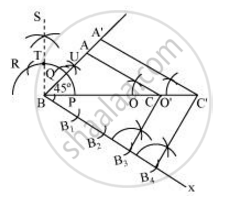
वांछित त्रिभुज को निम्नानुसार खींचा जा सकता है।
चरण 1
एक ΔABC खींचिए जिसकी भुजा BC = 7 सेमी, B = 45°, C = 30° हो।
चरण 2
शीर्ष A के विपरीत दिशा में BC से न्यून कोण बनाते हुए एक किरण BX खींचिए।
चरण 3
BX पर 4 अंक (चूंकि 4 में 4 और 3 में बड़ा है), B1, B2, B3, B4 का पता लगाएँ।
चरण 4
B3C. से जुड़ें। B4 से होकर B3C के समांतर एक रेखा खींचिए जो विस्तारित BC को C' पर प्रतिच्छेद करती है।
चरण 5
C' से होकर AC के समांतर एक रेखा खींचिए जो विस्तारित रेखाखंड को C' पर काटती है। अभीष्ट त्रिभुज A'BC' है।
औचित्य
निर्माण को सिद्ध करके उचित ठहराया जा सकता है
`A'B = 4/3 AB, BC' = 4/3BC , A'C' = 4/3 AC`
n ΔABC and ΔA'BC',
∠ABC = ∠A'BC' (सामान्य)
∠ACB = ∠A'C'B (सभी तरीके से)
∴ ΔABC ∼ ΔA'BC' (AA समानता मानदंड)
`=>(AB)/(A'B) = (BC)/(BC') = (AC)/(A'C') ....1`
In ΔBB3C and ΔBB4C',
∠B3BC = ∠B4BC' (सामान्य)
∠BB3C = ∠BB4C' (सभी तरीके से)
∴ ΔBB3C ∼ ΔBB4C' (AA समानता मानदंड)
`=>(BC)/(BC') = `
`=>(BC)/(BC') = 3/4 ...(2)`
समीकरणों (1) और (2) की तुलना करने पर, हम प्राप्त करते हैं
`(AB)/(A'B) = (BC)/(BC')=(AC)/(A'C') = 3/4`
`=> A'B = 4/3 AB, BC' = 4/3 BC, A'C' = 4/3 AC`
यह निर्माण को सही ठहराता है।
APPEARS IN
संबंधित प्रश्न
आधार 8 सेमी और ऊँचाई 4 सेमी एक समद्विबाहु त्रिभुज की रचना कीजिए और फिर एक अन्य त्रिभुज की रचना कीजिए, जिसकी भुजा समद्विबाहु त्रिभुज की संगत भुजाओं की `1 1/2` गुणा है।निर्माण का औचित्य बताइए
एक रेखाखंड AB को 4 : 7 के अनुपात में विभाजित करने के लिए, पहले एक किरण AX इस प्रकार खींची जाती है कि ∠BAX एक न्यून कोण हो और फिर किरण AX पर समान दूरियों पर बिंदु A1, A2, A3, .... अंकित किये जाते हैं और बिंदु B को निम्नलिखित से मिलाया जाता है।
एक रेखाखंड AB को 5 : 6 के अनुपात में विभाजित करने के लिए, एक किरण AX खींचिए ताकि ∠BAX एक न्यून कोण हो, फिर किरण BY किरण AX के समांतर विपरीत दिशा में खींचिए। इसके बाद AX और BY किरणों पर क्रमशः समान दूरियों पर बिंदु A1, A2, A3, ... और B1, B2, B3, ... अंकित किये जाएँ। फिर जिन बिंदुओं को मिलाया जाता है वे हैं।
एक दिये हुए त्रिभुज के समरूप एक ऐसे त्रिभुज की रचना करने के लिए जिसकी भुजाएँ ΔABC की संगत भुजाओं का `7/3` हों, BC से एक न्यून कोण बनाती हुई एक किरण BX खींचिए, ताकि X भुजा BC के सापेक्ष A के विपरीत ओर स्थित हो। BX पर समान दूरियों पर बिंदु B1, B2, ...., B7, अंकित कीजिए, B3 को C से मिलाइए और फिर B3C के समांतर एक रेखाखंड B6C' खींचा जाता है, जबकि बिंदु C' बढ़ाई गयी भुजा BC पर स्थित है। अंत में, AC के समांतर रेखाखंड A'C' खींचा जाता है।
लंबाई 7 cm का एक रेखाखंड खींचिए। इस पर स्थित एक बिंदु P ज्ञात कीजिए जो इस रेखाखंड को 3:5 के अनुपात में विभाजित करे।
एक समकोण त्रिभुज ABC खींचिए, जिसमें BC = 12 cm, AB = 5 cm और ∠B = 90° है। इस त्रिभुज के समरूप एक त्रिभुज की रचना कीजिए, जिसका स्केल गुणक `2/3` हो। क्या नया त्रिभुज भी एक समकोण त्रिभुज है?
एक त्रिभुज ABC खींचिए, जिसमें BC = 6 cm, CA = 5 cm और AB = 4 cm है। इस त्रिभुज के समरूप और स्केल गुणक `5/3` के एक त्रिभुज की रचना कीजिए।
दो रेखाखंडों AB और AC के बीच का कोण 60° है, जहाँ AB = 5 cm और AC = 7 cm है। AB और AC पर क्रमश : बिंदु P और Q इस प्रकार निर्धारित कीजिए कि AP = `3/4` AB और AQ = `1/4` AC हो। P और Q को मिलाइए तथा PQ की लंबाई ज्ञात कीजिए।
एक समद्विबाहु त्रिभुज ABC खींचिए, जिसमें AB = AC = 6 cm और BC = 5 cm है। ΔABC के समरूप, एक त्रिभुज PQR की रचना कीजिए, जिसमें PQ = 8 cm हो।अपनी रचना का औचित्य भी दीजिए।
एक त्रिभुज ABC खींचिए, जिसमें AB = 5 cm, BC = 6 cm और ∠ABC = 60° है। ΔABC के समरूप, स्केल गुणक `5/7` के एक त्रिभुज की रचना कीजिए। रचना का औचित्य दीजिए।
