Advertisements
Advertisements
प्रश्न
Examine the continuity of the following:
e2x + x2
उत्तर
Let f(x) = e2x + x2
Clearly, f(x) is defined for all points in R.
Let x0 be an arbitrary point in R.
`lim_(x -> x_0) f(x) = lim_(x -> x0) ("e"(2x) + x^2)`
= `"e"^(2x_0) + x_0^2` ........(1)
`f(x_0) = "e"^(2x_0) + x_0^2` ........(2)
From equations (1) and (2) we have,
The limit of the function f(x) exist at x = x0 and is equal to the value of the function f(x) at x – x0.
Since x0 is an arbitrary point in R, the above is true for all points in R.
Hence f(x) satisfies all conditions for continuity.
Hence f(x) is continuous at all points of R.
APPEARS IN
संबंधित प्रश्न
Examine the continuity of the following:
x . log x
Examine the continuity of the following:
`sinx/x^2`
Examine the continuity of the following:
`(x^2 - 16)/(x + 4)`
Examine the continuity of the following:
`|x - 2|/|x + 1|`
Examine the continuity of the following:
cot x + tan x
Find the points of discontinuity of the function f, where `f(x) = {{:(4x + 5",", "if", x ≤ 3),(4x - 5",", "if", x > 3):}`
Find the points of discontinuity of the function f, where `f(x) = {{:(x + 2",", "if", x ≥ 2),(x^2",", "if", x < 2):}`
Find the points of discontinuity of the function f, where `f(x) = {{:(sinx",", 0 ≤ x ≤ pi/4),(cos x",", pi/4 < x < pi/2):}`
Show that the function `{{:((x^3 - 1)/(x - 1)",", "if" x ≠ 1),(3",", "if" x = 1):}` is continuous om `(- oo, oo)`
For what value of `alpha` is this function `f(x) = {{:((x^4 - 1)/(x - 1)",", "if" x ≠ 1),(alpha",", "if" x = 1):}` continuous at x = 1?
Let `f(x) = {{:(0",", "if" x < 0),(x^2",", "if" 0 ≤ x ≤ 2),(4",", "if" x ≥ 2):}`. Graph the function. Show that f(x) continuous on `(- oo, oo)`
Find the points at which f is discontinuous. At which of these points f is continuous from the right, from the left, or neither? Sketch the graph of f.
`f(x) = {{:(2x + 1",", "if" x ≤ - 1),(3x",", "if" - 1 < x < 1),(2x - 1",", "if" x ≥ 1):}`
Find the points at which f is discontinuous. At which of these points f is continuous from the right, from the left, or neither? Sketch the graph of f.
`f(x) = {{:((x - 1)^3",", "if" x < 0),((x + 1)^3",", "if" x ≥ 0):}`
Which of the following functions f has a removable discontinuity at x = x0? If the discontinuity is removable, find a function g that agrees with f for x ≠ x0 and is continuous on R.
`f(x) = (x^3 + 64)/(x + 4), x_0` = – 4
State how continuity is destroyed at x = x0 for the following graphs.
State how continuity is destroyed at x = x0 for the following graphs.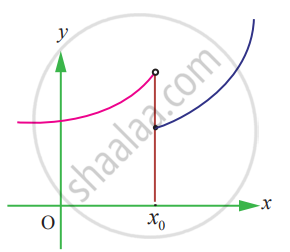
Choose the correct alternative:
If f : R → R is defined by `f(x) = [x - 3] + |x - 4|` for x ∈ R then `lim_(x -> 3^-) f(x)` is equal to
Choose the correct alternative:
The value of `lim_(x -> "k") x - [x]`, where k is an integer is
Choose the correct alternative:
The function `f(x) = {{:((x^2 - 1)/(x^3 + 1), x ≠ - 1),("P", x = -1):}` is not defined for x = −1. The value of f(−1) so that the function extended by this value is continuous is
Choose the correct alternative:
Let f be a continuous function on [2, 5]. If f takes only rational values for all x and f(3) = 12, then f(4.5) is equal to
