Advertisements
Advertisements
प्रश्न
Find the area of elipse `x^2/a^2+y^2/b^2=1`
उत्तर
equation of elipse `x^2/a^2+y^2/b^2=1`
Clearly the area of elipse is 4 times the area of region OPQD as show in the figure.For the region.Limits of integration are x=0 and x=a
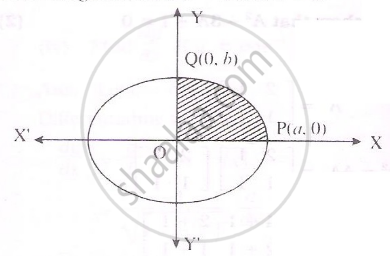
From the elipse
`y^2/b^2=1-x^2/a^2=(a^2-x^2)/a^2`
`therefore y^2=b^2/a^2(a^2-x^2)`
`y=+-b/a(a^2-x^2)^(1/2)`
`y=b/a(a^2-x^2)^(1/2)`
We know
`A=4int_0^1ydx`
`=int_0^ab/a(a^2-x^2)^(1/2)dx`
`=(4b)/a[x/2(a^2-x^2)^(1/2)+a^2/2sin^(-1)(x/a)]_0^a`
`=(4b)/a[a^2/2 pi/2-0]`
`=ab pi `
APPEARS IN
संबंधित प्रश्न
Find the area bounded by the curve y = x4, x-axis and lines x = 1 and x = 5.
Evaluate : `int _0^(pi/4) 1/(1 + "x"^2) "dx"`
Evaluate `int _0^l "x" (1 - "x")^(3/2) "dx"`
Evaluate : `int_3^9 [root(3)(12-x)]/[ root(3)(x) + root(3)(12 - x)]`
If y = 5x + xx, Find `(dy)/(dx)`.
Evaluate `int_0^1 (x(sin^-1 x)^2)/sqrt(1 - x^2)` dx
If f(x) = `("e"^(2"x") - 1)/"ax"` , for x < 0 , a ≠ 0
= 1 for x = 0
= `("log" (1 + 7"x"))/"bx"` , for x > 0 , b ≠ 0
is continuous at x = 0, then find a and b.
Find the volume of a solid obtained by the complete revolution of the ellipse `x^2/36 + y^2/25 = 1` about X-axis.
Find the area of the ellipse `x^2/a^2 + y^2/b^2 = 1`
The expenditure Ec of a person with income I is given by Ec = (0.000035)I2 +
(0.045)I. Find marginal propensity to consume (MPC) and marginal propensity to save (MPS) when I = 5000. Also find A(average) PC and A(average) PS.
Let X = amount of time for which a book is taken out of a college library by a randomly selected student and suppose X has p.d.f.
`f(x)={(0.5x",",0≤x≤2,,),(0",","otherwise",,):}`
Calculate (a) P (X ≤ 1) (b) P (0.5 ≤ X ≤ 1.5)
Find the area of the region bounded by the lines 2y + x = 8, x = 2 and x = 4.
Evaluate : `int e^x [(x + 3)/(x + 4)^2] dx`
Find `(dy)/(dx)` if x = a cosec θ, y = b cot θ at θ = `π/4`
