Advertisements
Advertisements
प्रश्न
Find the volume of a solid obtained by the complete revolution of the ellipse `x^2/36 + y^2/25 = 1` about X-axis.
उत्तर
From the equation of the ellipse
`x^2/36 + y^2/25 = 1`
`y^2 = 25/36 (36 - x^2)`
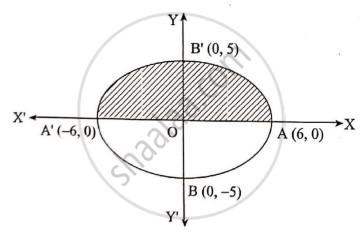
Lel V be the required volume of the solid obtained by revolving the ellipse about major axis i.e. X-axis.
V = `pi∫_-6^6 y^2` dx
= `∫_-6^6 25/36(36 - x^2)` dx
= `(25pi)/36 .2 ∫_-6^6 (36 - x^2)` dx ....(by property)
= `(25pi)/18 [36x - x^3/3]_0^6`
= `(25pi)/18 [36(6) - 6^3/3 - 0]`
= `(25pi)/18[144]`
V = 200π cubic units.
APPEARS IN
संबंधित प्रश्न
Find the area of elipse `x^2/a^2+y^2/b^2=1`
Find the area bounded by the curve y = x4, x-axis and lines x = 1 and x = 5.
Evaluate : `int _0^(pi/4) 1/(1 + "x"^2) "dx"`
Evaluate `int _0^l "x" (1 - "x")^(3/2) "dx"`
If y = 5x + xx, Find `(dy)/(dx)`.
Evaluate `int_0^1 (x(sin^-1 x)^2)/sqrt(1 - x^2)` dx
If f(x) = `("e"^(2"x") - 1)/"ax"` , for x < 0 , a ≠ 0
= 1 for x = 0
= `("log" (1 + 7"x"))/"bx"` , for x > 0 , b ≠ 0
is continuous at x = 0, then find a and b.
Find the area of the ellipse `x^2/a^2 + y^2/b^2 = 1`
The expenditure Ec of a person with income I is given by Ec = (0.000035)I2 +
(0.045)I. Find marginal propensity to consume (MPC) and marginal propensity to save (MPS) when I = 5000. Also find A(average) PC and A(average) PS.
Let X = amount of time for which a book is taken out of a college library by a randomly selected student and suppose X has p.d.f.
`f(x)={(0.5x",",0≤x≤2,,),(0",","otherwise",,):}`
Calculate (a) P (X ≤ 1) (b) P (0.5 ≤ X ≤ 1.5)
Evaluate : `int e^x [(x + 3)/(x + 4)^2] dx`
Find `(dy)/(dx)` if x = a cosec θ, y = b cot θ at θ = `π/4`
