Advertisements
Advertisements
प्रश्न
Find the area of a parallelogram ABCD if three of its vertices are A(2, 4), B(2 + \[\sqrt{3}\] , 5) and C(2, 6).
उत्तर
It is given that A(2, 4), B(2 + \[\sqrt{3}\] , 5) and C(2, 6) are the vertices of the parallelogram ABCD.
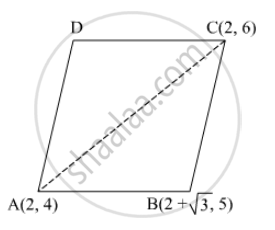
We know that the diagonal of a parallelogram divides it into two triangles having equal area.
∴ Area of the parallogram ABCD = 2 × Area of the ∆ABC
Now,
\[\text{ ar} \left( ∆ ABC \right) = \frac{1}{2}\left| x_1 \left( y_2 - y_3 \right) + x_2 \left( y_3 - y_1 \right) + x_3 \left( y_1 - y_2 \right) \right|\]
\[ = \frac{1}{2}\left| 2\left( 5 - 6 \right) + \left( 2 + \sqrt{3} \right)\left( 6 - 4 \right) + 2\left( 4 - 5 \right) \right|\]
\[ = \frac{1}{2}\left| - 2 + 4 + 2\sqrt{3} - 2 \right|\]
\[ = \frac{1}{2} \times 2\sqrt{3}\]
\[ = \sqrt{3}\text{ square units } \]
∴ Area of the parallogram ABCD = 2 × Area of the ∆ABC = 2 × \[\sqrt{3}\] = 2 \[\sqrt{3}\] square units
APPEARS IN
संबंधित प्रश्न
Prove that the points (−2, 5), (0, 1) and (2, −3) are collinear.
The coordinates of the point P are (−3, 2). Find the coordinates of the point Q which lies on the line joining P and origin such that OP = OQ.
The three vertices of a parallelogram are (3, 4) (3, 8) and (9, 8). Find the fourth vertex.
If two opposite vertices of a square are (5, 4) and (1, −6), find the coordinates of its remaining two vertices.
If G be the centroid of a triangle ABC, prove that:
AB2 + BC2 + CA2 = 3 (GA2 + GB2 + GC2)
Find the coordinates of the point where the diagonals of the parallelogram formed by joining the points (-2, -1), (1, 0), (4, 3) and(1, 2) meet
Three consecutive vertices of a parallelogram are (-2,-1), (1, 0) and (4, 3). Find the fourth vertex.
Find the ratio in which the line segment joining (-2, -3) and (5, 6) is divided by x-axis Also, find the coordinates of the point of division in each case.
The line joining the points (2, 1) and (5, -8) is trisected at the points P and Q. If point P lies on the line 2x - y + k = 0. Find the value of k.
If the point C ( - 2,3) is equidistant form the points A (3, -1) and Bx (x ,8) , find the value of x. Also, find the distance between BC
Show that the points A(3,0), B(4,5), C(-1,4) and D(-2,-1) are the vertices of a rhombus. Find its area.
Find the coordinates of the midpoints of the line segment joining
P(-11,-8) and Q(8,-2)
The midpoint P of the line segment joining points A(-10, 4) and B(-2, 0) lies on the line segment joining the points C(-9, -4) and D(-4, y). Find the ratio in which P divides CD. Also, find the value of y.
Points (−4, 0) and (7, 0) lie
The abscissa of any point on y-axis is
Prove hat the points A (2, 3) B(−2,2) C(−1,−2), and D(3, −1) are the vertices of a square ABCD.
\[A\left( 6, 1 \right) , B(8, 2) \text{ and } C(9, 4)\] are three vertices of a parallelogram ABCD . If E is the mid-point of DC , find the area of \[∆\] ADE.
what is the value of \[\frac{a^2}{bc} + \frac{b^2}{ca} + \frac{c^2}{ab}\] .
Which of the points P(0, 3), Q(1, 0), R(0, –1), S(–5, 0), T(1, 2) do not lie on the x-axis?
The coordinates of the point where the line 2y = 4x + 5 crosses x-axis is ______.
